


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-11-2019
Date: 20-9-2020
Date: 17-12-2020
|
The modular group Gamma is the set of all transformations 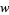 of the form
of the form
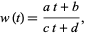 |
where 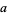 ,
, 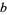 ,
, 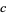 , and
, and 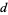 are integers and
are integers and 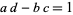 .
.
A 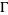 -modular function is then defined (Borwein and Borwein 1987, p. 114) as a function
-modular function is then defined (Borwein and Borwein 1987, p. 114) as a function 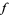 that satisfies:
that satisfies:
1. 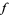 is meromorphic in the upper half-plane
is meromorphic in the upper half-plane 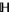 .
.
2. 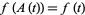 for all
for all 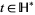 , where
, where 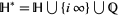 .
.
3. 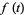 tends to a limit (possibly infinite in the sense that
tends to a limit (possibly infinite in the sense that 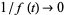 ) as
) as 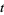 tends to the vertices of the fundamental region
tends to the vertices of the fundamental region 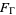 where the approach is from within the fundamental region
where the approach is from within the fundamental region 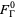 . (In the case
. (In the case 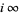 , convergence is uniform in
, convergence is uniform in ![R[x+iy]](http://mathworld.wolfram.com/images/equations/Gamma-ModularFunction/Inline20.gif) as
as 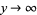 .) The vertices of the fundamental region are
.) The vertices of the fundamental region are 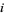 ,
, 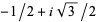 and
and 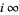 . Since
. Since 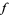 is meromorphic in
is meromorphic in 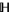 , this condition is automatically satisfied at
, this condition is automatically satisfied at 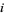 and
and 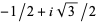 and need be checked only at
and need be checked only at 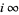 .
.
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|