


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-12-2019
Date: 9-1-2021
Date: 18-11-2019
|
A product involving an infinite number of terms. Such products can converge. In fact, for positive 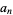 , the product
, the product 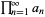 converges to a nonzero number iff
converges to a nonzero number iff 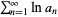 converges.
converges.
Infinite products can be used to define the cosine
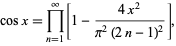 |
(1) |
gamma function
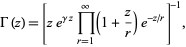 |
(2) |
sine, and sinc function. They also appear in polygon circumscribing,
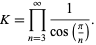 |
(3) |
An interesting infinite product formula due to Euler which relates 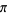 and the
and the 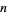 th prime
th prime 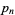 is
is
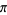 |
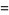 |
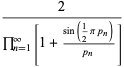 |
(4) |
 |
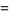 |
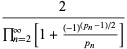 |
(5) |
(Blatner 1997). Knar's formula gives a functional equation for the gamma function 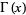 in terms of the infinite product
in terms of the infinite product
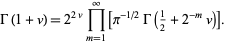 |
(6) |
A regularized product identity is given by
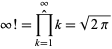 |
(7) |
(Muñoz Garcia and Pérez-Marco 2003, 2008).
Mellin's formula states
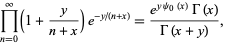 |
(8) |
where 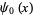 is the digamma function and
is the digamma function and 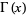 is the gamma function.
is the gamma function.
The following class of products
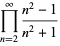 |
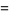 |
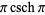 |
(9) |
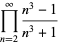 |
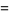 |
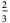 |
(10) |
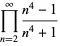 |
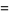 |
![-1/2pisinhpicsc[(-1)^(1/4)pi]csc[(-1)^(3/4)pi]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline24.gif) |
(11) |
 |
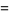 |
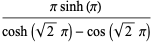 |
(12) |
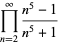 |
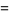 |
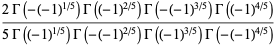 |
(13) |
(Borwein et al. 2004, pp. 4-6), where 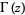 is the gamma function, the first of which is given in Borwein and Corless (1999), can be done analytically. In particular, for
is the gamma function, the first of which is given in Borwein and Corless (1999), can be done analytically. In particular, for 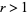 ,
,
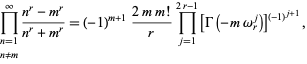 |
(14) |
where 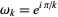 (Borwein et al. 2004, pp. 6-7). It is not known if (13) is algebraic, although it is known to satisfy no integer polynomial with degree less than 21 and Euclidean norm less than
(Borwein et al. 2004, pp. 6-7). It is not known if (13) is algebraic, although it is known to satisfy no integer polynomial with degree less than 21 and Euclidean norm less than 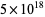 (Borwein et al. 2004, p. 7).
(Borwein et al. 2004, p. 7).
Products of the following form can be done analytically,
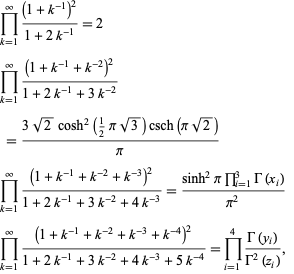 |
(15) |
where 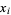 ,
, 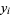 , and
, and 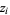 are the roots of
are the roots of
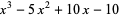 |
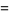 |
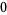 |
(16) |
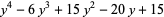 |
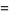 |
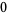 |
(17) |
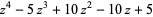 |
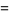 |
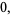 |
(18) |
respectively, can also be done analytically. Note that (17) and (18) were unknown to Borwein and Corless (1999). These are special cases of the result that
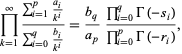 |
(19) |
if 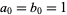 and
and 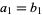 , where
, where 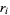 is the
is the 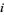 th root of
th root of 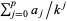 and
and 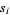 is the
is the 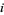 th root of
th root of 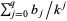 (P. Abbott, pers. comm., Mar. 30, 2006).
(P. Abbott, pers. comm., Mar. 30, 2006).
For 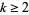 ,
,
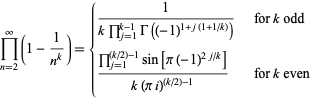 |
(20) |
(D. W. Cantrell, pers. comm., Apr. 18, 2006). The first few explicit cases are
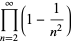 |
 |
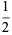 |
(21) |
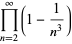 |
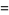 |
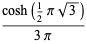 |
(22) |
 |
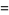 |
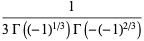 |
(23) |
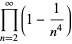 |
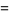 |
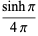 |
(24) |
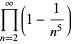 |
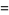 |
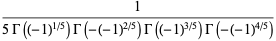 |
(25) |
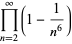 |
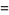 |
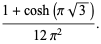 |
(26) |
These are a special case of the general formula
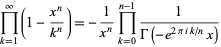 |
(27) |
(Prudnikov et al. 1986, p. 754).
Similarly, for 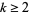 ,
,
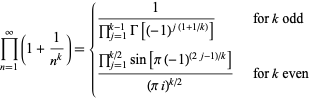 |
(28) |
(D. W. Cantrell, pers. comm., Mar. 29, 2006). The first few explicit cases are
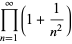 |
 |
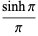 |
(29) |
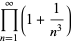 |
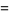 |
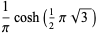 |
(30) |
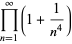 |
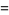 |
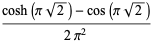 |
(31) |
 |
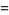 |
![-(sin[(-1)^(1/4)pi]sin[(-1)^(3/4)pi])/(pi^2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline86.gif) |
(32) |
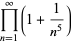 |
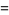 |
![|Gamma[exp(2/5pii)]Gamma[exp(6/5pii)]|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline89.gif) |
(33) |
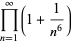 |
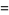 |
![(sinhpi[coshpi-cos(sqrt(3)pi)])/(2pi^3).](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline92.gif) |
(34) |
The d-analog expression
![[infty!]_d=product_(n=3)^infty(1-(2^d)/(n^d))](http://mathworld.wolfram.com/images/equations/InfiniteProduct/NumberedEquation13.gif) |
(35) |
also has closed form expressions,
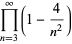 |
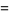 |
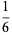 |
(36) |
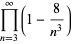 |
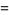 |
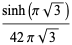 |
(37) |
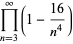 |
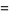 |
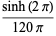 |
(38) |
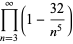 |
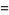 |
![|Gamma[exp(1/5pii)]Gamma[2exp(7/5pii)]|^(-2).](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline104.gif) |
(39) |
General expressions for infinite products of this type include
![product_(n=1)^(infty)[1-(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline105.gif) |
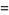 |
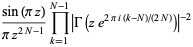 |
(40) |
![product_(n=1)^(infty)[1+(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline108.gif) |
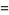 |
![1/(z^(2N))product_(k=1)^(N)|Gamma(ze^(pii[2(k-N)-1]/(2N)))|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline110.gif) |
(41) |
![product_(n=1)^(infty)[1-(z/n)^(2N+1)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline111.gif) |
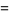 |
![1/(Gamma(1-z)z^(2N))product_(k=1)^(N)|Gamma(ze^(pii[2(k-N)-1]/(2N+1)))|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline113.gif) |
(42) |
![product_(n=1)^(infty)[1+(z/n)^(2N+1)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline114.gif) |
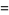 |
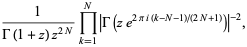 |
(43) |
where 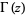 is the gamma function and
is the gamma function and 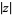 denotes the complex modulus (Kahovec). (40) and (41) can also be rewritten as
denotes the complex modulus (Kahovec). (40) and (41) can also be rewritten as
![product_(n=1)^(infty)[1-(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline119.gif) |
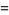 |
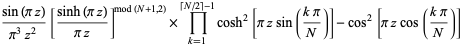 |
(44) |
![product_(n=1)^(infty)[1+(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline122.gif) |
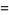 |
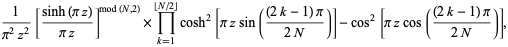 |
(45) |
where 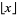 is the floor function,
is the floor function, ![[x]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline126.gif) is the ceiling function, and
is the ceiling function, and 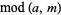 is the modulus of
is the modulus of 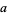 (mod
(mod 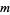 ) (Kahovec).
) (Kahovec).
Infinite products of the form
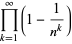 |
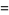 |
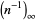 |
(46) |
 |
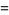 |
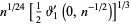 |
(47) |
converge for 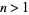 , where
, where 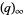 is a q-Pochhammer symbol and
is a q-Pochhammer symbol and 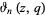 is a Jacobi theta function. Here, the
is a Jacobi theta function. Here, the 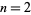 case is exactly the constant
case is exactly the constant 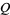 encountered in the analysis of digital tree searching.
encountered in the analysis of digital tree searching.
Other products include
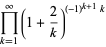 |
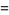 |
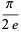 |
(48) |
||
 |
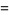 |
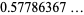 |
(49) |
||
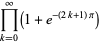 |
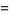 |
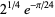 |
(50) |
||
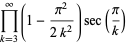 |
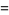 |
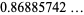 |
 |
 |
(51) |
(OEIS A086056 and A247559; Prudnikov et al. 1986, p. 757). Note that Prudnikov et al. (1986, p. 757) also incorrectly give the product
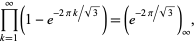 |
(52) |
where 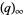 is a q-Pochhammer symbol, as
is a q-Pochhammer symbol, as 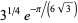 , which differs from the correct result by
, which differs from the correct result by 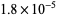 .
.
The following analogous classes of products can also be done analytically (J. Zúñiga, pers. comm., Nov. 9, 2004), where again 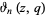 is a Jacobi theta function,
is a Jacobi theta function,
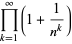 |
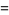 |
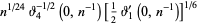 |
(53) |
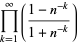 |
 |
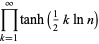 |
(54) |
 |
 |
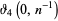 |
(55) |
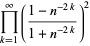 |
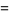 |
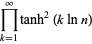 |
(56) |
 |
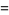 |
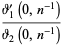 |
(57) |
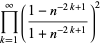 |
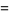 |
![product_(k=1)^(infty)tanh^2[(k-1/2)lnn]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline176.gif) |
(58) |
 |
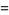 |
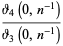 |
(59) |
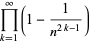 |
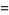 |
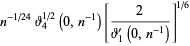 |
(60) |
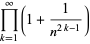 |
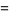 |
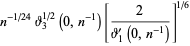 |
(61) |
![product_(k=1)^(infty)[1+(-1)^(k-1)b/(k+a)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline186.gif) |
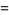 |
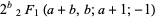 |
(62) |
 |
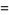 |
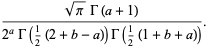 |
(63) |
The first of these can be used to express the Fibonacci factorial constant in closed form.
A class of infinite products derived from the Barnes G-function is given by
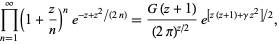 |
(64) |
where 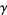 is the Euler-Mascheroni constant. For
is the Euler-Mascheroni constant. For 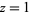 , 2, 3, and 4, the explicit products are given by
, 2, 3, and 4, the explicit products are given by
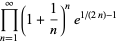 |
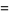 |
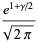 |
(65) |
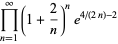 |
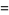 |
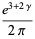 |
(66) |
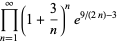 |
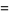 |
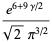 |
(67) |
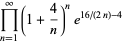 |
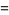 |
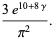 |
(68) |
The interesting identities
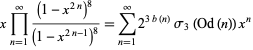 |
(69) |
(Ewell 1995, 2000), where 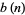 is the exponent of the exact power of 2 dividing
is the exponent of the exact power of 2 dividing 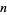 ,
, 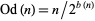 is the odd part of
is the odd part of 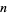 ,
, 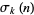 is the divisor function of
is the divisor function of 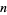 , and
, and
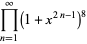 |
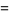 |
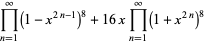 |
(70) |
 |
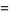 |
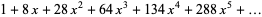 |
(71) |
(OEIS A101127; Jacobi 1829; Ford et al. 1994; Ewell 1998, 2000), the latter of which is known as "aequatio identica satis abstrusa" in the string theory physics literature, arise is connection with the tau function.
An unexpected infinite product involving 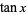 is given by
is given by
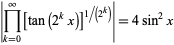 |
(72) |
(Dobinski 1876, Agnew and Walker 1947).
A curious identity first noted by Gosper is given by
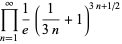 |
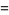 |
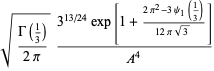 |
(73) |
 |
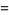 |
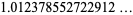 |
(74) |
(OEIS A100072), where 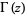 is the gamma function,
is the gamma function, 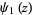 is the trigamma function, and
is the trigamma function, and 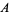 is the Glaisher-Kinkelin constant.
is the Glaisher-Kinkelin constant.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 75, 1972.
Agnew, R. P. and Walker, R. J. "A Trigonometric Infinite Product." Amer. Math. Monthly 54, 206-211, 1947.
Arfken, G. "Infinite Products." §5.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 346-351, 1985.
Blatner, D. The Joy of Pi. New York: Walker, p. 119, 1997.
Borwein, J.; Bailey, D.; and Girgensohn, R. "Two Products." §1.2 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 4-7, 2004.
Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.
Dobinski, G. "Product einer unendlichen Factorenreihe." Archiv Math. u. Phys. 59, 98-100, 1876.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 6, 1981.
Ewell, J. A. "Arithmetical Consequences of a Sextuple Product Identity." Rocky Mtn. J. Math. 25, 1287-1293, 1995.
Ewell, J. A. "A Note on a Jacobian Identity." Proc. Amer. Math. Soc. 126, 421-423, 1998.
Ewell, J. A. "New Representations of Ramanujan's Tau Function." Proc. Amer. Math. Soc. 128, 723-726, 2000.
Finch, S. R. "Kepler-Bouwkamp Constant." §6.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 428-429, 2003.
Ford, D.; McKay, J.; and Norton, S. P. "More on Replicable Functions." Commun. Alg. 22, 5175-5193, 1994.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Jacobi, C. G. J. "E formulis (7.),(8.) sequitur aequatio identica satis abstrusa: (14.) 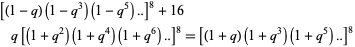 ." Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, 1829. Reprinted in Gesammelte Werke, Band. 1. Providence, RI: Amer. Math. Soc., p. 147, 1969.
." Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, 1829. Reprinted in Gesammelte Werke, Band. 1. Providence, RI: Amer. Math. Soc., p. 147, 1969.
Jeffreys, H. and Jeffreys, B. S. "Infinite Products." §1.14 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 52-53, 1988.
Krantz, S. G. "The Concept of an Infinite Product." §8.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 104-105, 1999.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 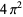 ." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 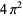 ." Commun. Math. Phys. 277, 69-81, 2008.
." Commun. Math. Phys. 277, 69-81, 2008.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. "Infinite Products." §6.2 in Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, pp. 753-757, 1986.
Ritt, J. F. "Representation of Analytic Functions as Infinite Products." Math. Z. 32, 1-3, 1930.
Sloane, N. J. A. Sequences A048651, A086056, A100072, A100220, A100221, A100222, A101127, and A247559 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. §7.5-7.6 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|