Farey Sequence

The Farey sequence 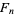 for any positive integer  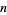is the set of irreducible rational numbers  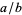with 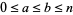 and 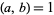 arranged in increasing order. The first few are

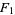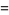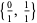			(1)
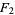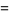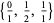			(2)
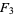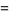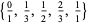			(3)
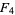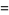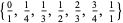			(4)
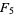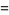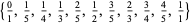			(5)

(OEIS A006842 and A006843). Except for 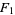, each  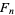has an odd number of terms and the middle term is always 1/2.

Let 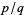, , 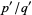and 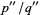 be three successive terms in a Farey series. Then

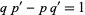(6)

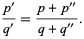(7)

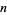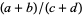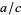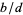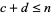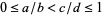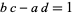These two statements are actually equivalent (Hardy and Wright 1979, p. 24). For a method of computing a successive sequence from an existing one of  terms, insert the mediant fraction  between terms  and  when  (Hardy and Wright 1979, pp. 25-26; Conway and Guy 1996; Apostol 1997). Given  with , let 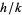 be the mediant of  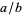and 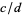. Then 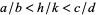, and these fractions satisfy the unimodular relations

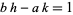(8)

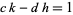(9)

(Apostol 1997, p. 99).

The number of terms 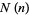 in the Farey sequence for the integer  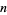is

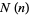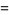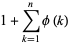			(10)
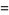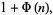			(11)

where 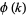 is the totient function and  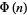is the summatory function of 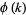, giving 2, 3, 5, 7, 11, 13, 19, ... (OEIS A005728). The asymptotic limit for the function  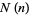is

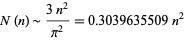(12)

(Vardi 1991, p. 155).

Ford circles provide a method of visualizing the Farey sequence. The Farey sequence 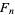 defines a subtree of the Stern-Brocot tree obtained by pruning unwanted branches (Graham et al. 1994).

The Season 2 episode "Bettor or Worse" (2006) of the television crime drama NUMB3RS features Farey sequences.

REFERENCES:

Apostol, T. M. "Farey Fractions." §5.4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 97-99, 1997.

Beiler, A. H. "Farey Tails." Ch. 16 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.

Bogomolny, A. "Farey Series, A Story." http://www.cut-the-knot.org/blue/FareyHistory.shtml.

Conway, J. H. and Guy, R. K. "Farey Fractions and Ford Circles." The Book of Numbers. New York: Springer-Verlag, pp. 152-154 and 156, 1996.

Devaney, R. "The Mandelbrot Set and the Farey Tree, and the Fibonacci Sequence." Amer. Math. Monthly 106, 289-302, 1999.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 155-158, 2005.

Farey, J. "On a Curious Property of Vulgar Fractions." London, Edinburgh and Dublin Phil. Mag. 47, 385, 1816.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 118-119, 1994.

Guy, R. K. "Mahler's Generalization of Farey Series." §F27 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 263-265, 1994.

Hardy, G. H. and Wright, E. M. "Farey Series and a Theorem of Minkowski." Ch. 3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 23-37, 1979.

Sloane, N. J. A. Sequences A005728/M0661, A006842/M0041, and A006843/M0081 in "The On-Line Encyclopedia of Integer Sequences."

Sylvester, J. J. "On the Number of Fractions Contained in Any Farey Series of Which the Limiting Number is Given." London, Edinburgh and Dublin Phil. Mag. (5th Series) 15, 251, 1883.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 155, 1991.