


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-10-2020
Date: 14-3-2020
Date: 19-10-2019
|
A conjecture due to Paul Erdős and E. G. Straus that the Diophantine equation
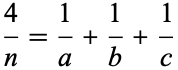 |
involving Egyptian fractions always can be solved (Obláth 1950, Rosati 1954, Bernstein 1962, Yamamoto 1965, Vaughan 1970, Guy 1994). Swett has established validity of the conjecture for all 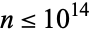 .
.
REFERENCES:
Bernstein, L "Zur Lösung der diophantischen Gleichung 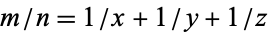 insbesondere im Falle
insbesondere im Falle 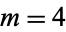 ." J. reine angew. Math. 211, 1-10, 1962.
." J. reine angew. Math. 211, 1-10, 1962.
Guy, R. K. "Egyptian Fractions." §D11 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 158-166, 1994.
Obláth, R. "Sur l'equation diophantienne 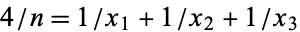 ." Mathesis 59, 308-316, 1950.
." Mathesis 59, 308-316, 1950.
Rosati, L. A. "Sull'equazione diofantea 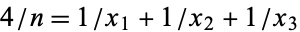 ." Boll. Un. Mat. Ital. 9, 59-63, 1954.
." Boll. Un. Mat. Ital. 9, 59-63, 1954.
Swett, A. "The Erdos-Strauss Conjecture." Rev. 10/28/99. http://math.uindy.edu/swett/esc.htm.
Vaughan, R. C. "On a Problem of Erdős, Straus and Schinzel." Mathematika 17, 193-198, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 29, 1986.
Yamamoto, K. "On the Diophantine Equation 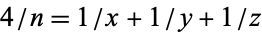 ." Mem. Fac. Sci. Kyushu U. Ser. A 19, 37-47, 1965.
." Mem. Fac. Sci. Kyushu U. Ser. A 19, 37-47, 1965.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|