Lucas Polynomial

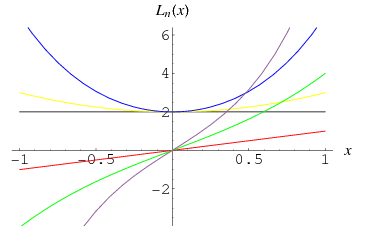
The Lucas polynomials are the 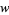-polynomials obtained by setting  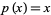and 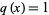 in the Lucas polynomial sequence. It is given explicitly by

(1)

The first few are

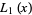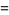			(2)
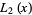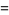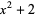			(3)
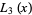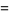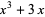			(4)
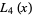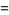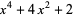			(5)
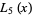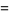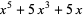			(6)

(OEIS A114525).

The Lucas polynomial is implemented in the Wolfram Language as LucasL[n, x].

The Lucas polynomial has generating function

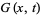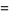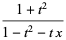			(7)
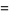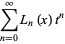			(8)
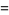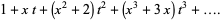			(9)

The derivative of 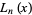 is given by

(10)

The Lucas polynomials have the divisibility property that 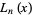 divides  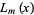iff 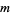 is an odd multiple of 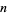. For prime 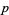,  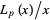is an irreducible polynomial. The zeros of  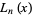are 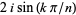 for 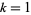, ..., 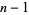. For prime 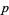, except for the root of 0, these roots are  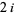times the imaginary part of the roots of the 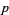th cyclotomic polynomial (Koshy 2001, p. 464).

The corresponding 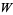 polynomials are called Fibonacci polynomials. The Lucas polynomials satisfy

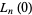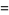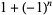			(11)
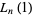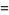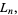			(12)

where the 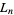s are Lucas numbers.

REFERENCES:

Koshy, T. Fibonacci and Lucas Numbers with Applications. New York: Wiley, 2001.

Sloane, N. J. A. Sequence A114525 in "The On-Line Encyclopedia of Integer Sequences."