


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-7-2019
Date: 18-8-2018
Date: 16-5-2018
|
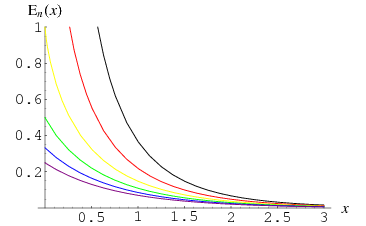
The 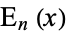 function is defined by the integral
function is defined by the integral
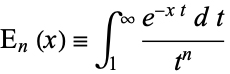 |
(1) |
and is given by the Wolfram Language function ExpIntegralE[n, x]. Defining 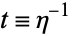 so that
so that 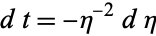 ,
,
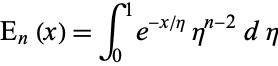 |
(2) |
For integer 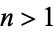 ,
,
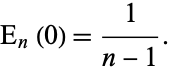 |
(3) |
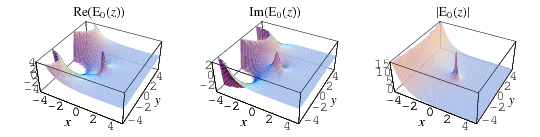
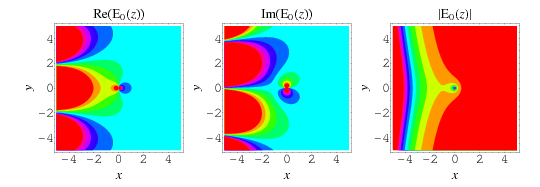
Plots in the complex plane are shown above for 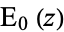 .
.
The special case 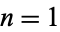 gives
gives
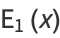 |
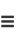 |
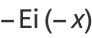 |
(4) |
 |
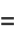 |
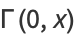 |
(5) |
 |
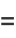 |
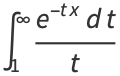 |
(6) |
 |
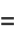 |
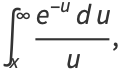 |
(7) |
where 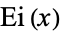 is the exponential integral and
is the exponential integral and 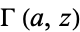 is an incomplete gamma function. It is also equal to
is an incomplete gamma function. It is also equal to
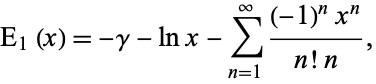 |
(8) |
where 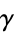 is the Euler-Mascheroni constant.
is the Euler-Mascheroni constant.
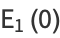 |
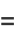 |
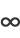 |
(9) |
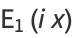 |
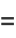 |
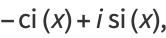 |
(10) |
where 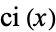 and
and 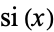 are the cosine integral and sine integral.
are the cosine integral and sine integral.
The function satisfies the recurrence relations
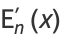 |
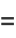 |
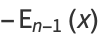 |
(11) |
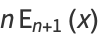 |
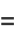 |
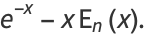 |
(12) |
In general, 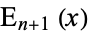 can be built up from the recurrence
can be built up from the recurrence
![E_n(x)=1/((n-1)!)[(-x)^(n-1)E_1(x)+e^(-x)sum_(s=0)^(n-2)(n-s-2)!(-x)^s].](http://mathworld.wolfram.com/images/equations/En-Function/NumberedEquation5.gif) |
(13) |
The series expansions is given by
![E_n(x)=x^(n-1)Gamma(1-n)+[-1/(1-n)+x/(2-n)-(x^2)/(2(3-n))+(x^3)/(6(4-n))-...]](http://mathworld.wolfram.com/images/equations/En-Function/NumberedEquation6.gif) |
(14) |
and the asymptotic expansion by
![E_n(x)=(e^(-x))/x[1-n/x+(n(n+1))/(x^2)+...].](http://mathworld.wolfram.com/images/equations/En-Function/NumberedEquation7.gif) |
(15) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Exponential Integral and Related Functions." Ch. 5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 227-233, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Exponential Integrals." §6.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 215-219, 1992.
Spanier, J. and Oldham, K. B. "The Exponential Integral Ei(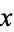 ) and Related Functions." Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987.
) and Related Functions." Ch. 37 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 351-360, 1987.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|