المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Null Function |
 1326
 02:47 صباحاً
date: 25-5-2019 |
Author : Bracewell, R. 
Book or Source : "Null Functions." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, , 1999. 
Page and Part : pp. 82-84|
Read More
Date: 24-6-2019
1313
Date: 30-3-2019
1469
Date: 21-7-2019
1536
|
A null function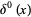 
satisfies
 |
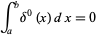(1) |
for all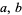 
, so
 |
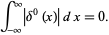(2) |
Like a delta function, they satisfy
 |
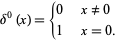(3) |
REFERENCES:
Bracewell, R. "Null Functions." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 82-84, 1999.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
