المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Elliptic Integral Singular Value--k_3 |
 1317
 02:52 صباحاً
date: 25-4-2019 |
Author : Ramanujan, S 
Book or Source : "Modular Equations and Approximations to pi." Quart. J. Pure. Appl. Math. 45 
Page and Part : ...|
Read More
Date: 22-4-2019
1829
Date: 14-10-2019
1158
Date: 30-3-2019
1615
|
The third singular value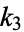 
, corresponding to
 |
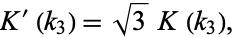(1) |
is given by
 |
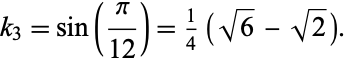(2) |
As shown by Legendre,
 |
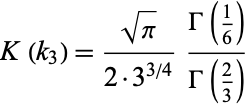(3) |
(Whittaker and Watson 1990, p. 525). In addition,
![E(k_3)=pi/(4sqrt(3))1/K+(sqrt(3)+1)/(2sqrt(3))K=1/4(pi/(sqrt(3)))^(1/2)[(1+1/(sqrt(3)))(Gamma(1/3))/(Gamma(5/6))+(2Gamma(5/6))/(Gamma(1/3))],](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek3/NumberedEquation4.gif) |
(4) |
and
 |
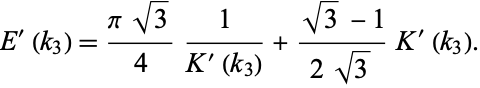(5) |
Summarizing,
![K[1/4(sqrt(6)-sqrt(2))]](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek3/Inline2.gif) |
 |
 |
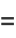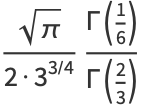(6) |
 |
 |
 |
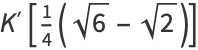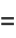(7) |
![E[1/4(sqrt(6)-sqrt(2))]](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek3/Inline8.gif) |
 |
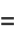![1/4(pi/(sqrt(3)))^(1/2)[(1+1/(sqrt(3)))(Gamma(1/3))/(Gamma(5/6))+(2Gamma(5/6))/(Gamma(1/3))]](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek3/Inline10.gif) |
(8) |
 |
 |
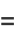![(sqrt(pi))/2[3^(3/4)(Gamma(2/3))/(Gamma(1/6))+(sqrt(3)-1)/(2·3^(3/4))(Gamma(1/6))/(Gamma(2/3))].](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek3/Inline13.gif) |
(9) |
(Whittaker and Watson 1990).
REFERENCES:
Ramanujan, S. "Modular Equations and Approximations to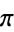 
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 525-527 and 535, 1990.
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
الزائرون يحيون ليلة الجمعة الأخيرة من شهر ربيع الآخر عند مرقد أبي الفضل العبّاس (عليه السلام)
|
|
|
