المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Gauss-Kummer Series |
 1835
 04:58 مساءً
date: 11-6-2019 |
Author : Sloane, N. J. A 
Book or Source : Sequences A056981 and A056982 in "The On-Line Encyclopedia of Integer Sequence 
Page and Part : ...|
Read More
Date: 20-7-2019
1803
Date: 21-9-2018
1874
Date: 18-8-2019
3176
|
 |
 |
 |
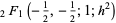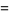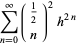(1) |
 |
 |
 |
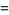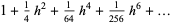(2) |
(OEIS A056981 and A056982), where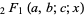 
is a hypergeometric function and 
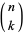is a binomial coefficient. The series can be derived using Kummer's quadratic transformation. The Gauss-Kummer series is closely related to the perimeter of an ellipse.
REFERENCES:
Sloane, N. J. A. Sequences A056981 and A056982 in "The On-Line Encyclopedia of Integer Sequence
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
