المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Equianharmonic Case |
 1357
 01:16 صباحاً
date: 22-4-2019 |
Author : Abramowitz, M. and Stegun, I. A 
Book or Source : "Equianharmonic Case (g_2=0, g_3=1)." §18.13 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New... 
Page and Part : ...|
Read More
Date: 9-9-2019
1074
Date: 24-3-2019
1466
Date: 18-8-2018
1865
|
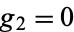and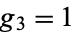 
. The corresponding real half-period is given by
 |
 |
 |
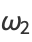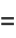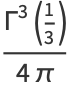(1) |
 |
 |
 |
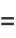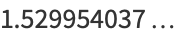(2) |
(OEIS A064582), known as the omega2-constant, where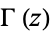 
is the gamma function. The other half-period is then given by
 |
 |
 |
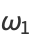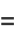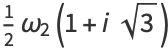(3) |
 |
 |
 |
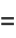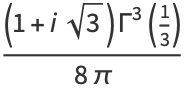(4) |
 |
 |
 |
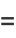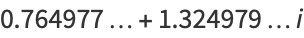(5) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Equianharmonic Case (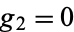
, 
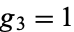)." §18.13 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 652-653, 1972.
Finch, S. R. "Gauss' Lemniscate Constant." §6.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 420-423, 2003.
Sloane, N. J. A. Sequences A064582, A094961, and A094962 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
