


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 28-8-2018
Date: 12-8-2018
|
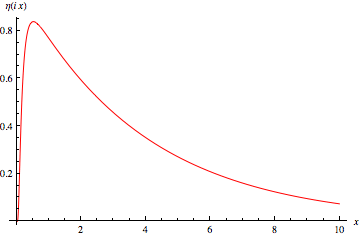 |
The Dedekind eta function is defined over the upper half-plane ![H={tau:I[tau]>0}](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/Inline1.gif) by
by
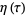 |
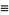 |
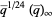 |
(1) |
 |
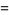 |
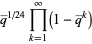 |
(2) |
 |
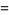 |
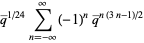 |
(3) |
 |
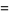 |
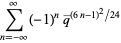 |
(4) |
 |
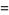 |
![q^_^(1/24){1+sum_(n=1)^(infty)(-1)^n[q^_^(n(3n-1)/2)+q^_^(n(3n+1)/2)]}](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/Inline16.gif) |
(5) |
 |
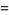 |
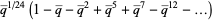 |
(6) |
(OEIS A010815), where 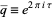 is the square of the nome
is the square of the nome 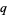 ,
,  is the half-period ratio, and
is the half-period ratio, and 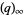 is a q-series (Weber 1902, pp. 85 and 112; Atkin and Morain 1993; Berndt 1994, p. 139).
is a q-series (Weber 1902, pp. 85 and 112; Atkin and Morain 1993; Berndt 1994, p. 139).
The Dedekind eta function is implemented in the Wolfram Language as DedekindEta[tau].
Rewriting the definition in terms of 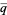 explicitly in terms of the half-period ratio
explicitly in terms of the half-period ratio  gives the product
gives the product
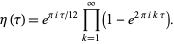 |
(7) |
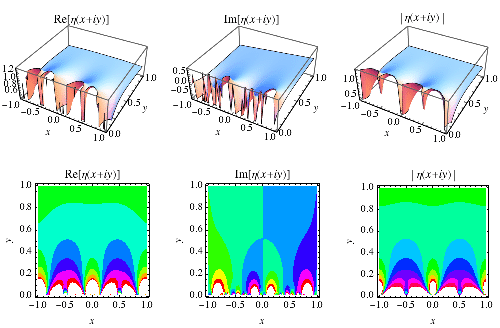 |
It is illustrated above in the complex plane.
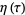 is a modular form first introduced by Dedekind in 1877, and is related to the modular discriminant of the Weierstrass elliptic function by
is a modular form first introduced by Dedekind in 1877, and is related to the modular discriminant of the Weierstrass elliptic function by
![Delta(tau)=(2pi)^(12)[eta(tau)]^(24)](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/NumberedEquation2.gif) |
(8) |
(Apostol 1997, p. 47).
A compact closed form for the derivative is given by
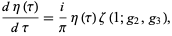 |
(9) |
where 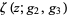 is the Weierstrass zeta function and
is the Weierstrass zeta function and 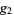 and
and 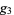 are the invariants corresponding to the half-periods
are the invariants corresponding to the half-periods 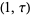 . The derivative of
. The derivative of 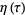 satisfies
satisfies
![-4piid/(dtau)ln[eta(tau)]=G_2(tau),](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/NumberedEquation4.gif) |
(10) |
where 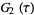 is an Eisenstein series, and
is an Eisenstein series, and
![d/(dtau)ln[eta(-1/tau)]=d/(dtau)ln[eta(tau)]+1/2d/(dtau)ln(-itau).](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/NumberedEquation5.gif) |
(11) |
A special value is given by
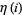 |
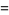 |
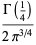 |
(12) |
 |
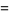 |
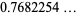 |
(13) |
(OEIS A091343), where 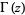 is the gamma function. Another special case is
is the gamma function. Another special case is
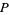 |
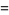 |
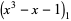 |
(14) |
 |
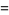 |
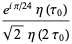 |
(15) |
 |
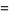 |
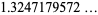 |
(16) |
where 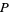 is the plastic constant,
is the plastic constant, 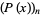 denotes a polynomial root, and
denotes a polynomial root, and 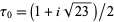 .
.
Letting 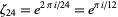 be a root of unity,
be a root of unity, 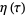 satisfies
satisfies
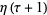 |
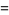 |
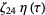 |
(17) |
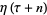 |
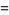 |
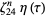 |
(18) |
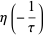 |
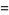 |
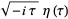 |
(19) |
where 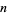 is an integer (Weber 1902, p. 113; Atkin and Morain 1993; Apostol 1997, p. 47). The Dedekind eta function is related to the Jacobi theta function
is an integer (Weber 1902, p. 113; Atkin and Morain 1993; Apostol 1997, p. 47). The Dedekind eta function is related to the Jacobi theta function 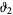 by
by
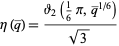 |
(20) |
(Weber 1902, Vol. 3, p. 112) and
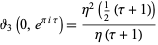 |
(21) |
(Apostol 1997, p. 91).
Macdonald (1972) has related most expansions of the form 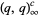 to affine root systems. Exceptions not included in Macdonald's treatment include
to affine root systems. Exceptions not included in Macdonald's treatment include 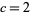 , found by Hecke and Rogers,
, found by Hecke and Rogers, 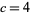 , found by Ramanujan, and
, found by Ramanujan, and 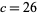 , found by Atkin (Leininger and Milne 1999). Using the Dedekind eta function, the Jacobi triple product identity
, found by Atkin (Leininger and Milne 1999). Using the Dedekind eta function, the Jacobi triple product identity
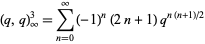 |
(22) |
can be written
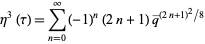 |
(23) |
(Jacobi 1829, Hardy and Wright 1979, Hirschhorn 1999, Leininger and Milne 1999).
Dedekind's functional equation states that if ![[a b; c d] in Gamma](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/Inline69.gif) , where
, where 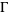 is the modular group Gamma,
is the modular group Gamma, 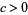 , and
, and 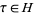 (where
(where 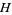 is the upper half-plane), then
is the upper half-plane), then
![eta((atau+b)/(ctau+d))=epsilon(a,b,c,d)[sqrt(-i(ctau+d))]eta(tau),](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/NumberedEquation10.gif) |
(24) |
where
![epsilon(a,b,c,d)=exp[pii((a+d)/(12c)+s(-d,c))],](http://mathworld.wolfram.com/images/equations/DedekindEtaFunction/NumberedEquation11.gif) |
(25) |
and
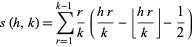 |
(26) |
is a Dedekind sum (Apostol 1997, pp. 52-57), with 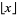 the floor function.
the floor function.
REFERENCES:
Apostol, T. M. "The Dedekind Eta Function." Ch. 3 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 47-73, 1997.
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Bhargava, S. and Somashekara, D. "Some Eta-Function Identities Deducible from Ramanujan's 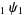 Summation." J. Math. Anal. Appl. 176, 554-560, 1993.
Summation." J. Math. Anal. Appl. 176, 554-560, 1993.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hirschhorn, M. D. "Another Short Proof of Ramanujan's Mod 5 Partition Congruences, and More." Amer. Math. Monthly 106, 580-583, 1999.
Jacobi, C. G. J. Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, p. 90, 1829.
Leininger, V. E. and Milne, S. C. "Expansions for 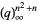 and Basic Hypergeometric Series in
and Basic Hypergeometric Series in 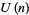 ." Discr. Math. 204, 281-317, 1999a.
." Discr. Math. 204, 281-317, 1999a.
Leininger, V. E. and Milne, S. C. "Some New Infinite Families of 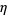 -Function Identities." Methods Appl. Anal. 6, 225-248, 1999b.
-Function Identities." Methods Appl. Anal. 6, 225-248, 1999b.
Köhler, G. "Some Eta-Identities Arising from Theta Series." Math. Scand. 66, 147-154, 1990.
Macdonald, I. G. "Affine Root Systems and Dedekind's 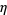 -Function." Invent. Math. 15, 91-143, 1972.
-Function." Invent. Math. 15, 91-143, 1972.
Ramanujan, S. "On Certain Arithmetical Functions." Trans. Cambridge Philos. Soc. 22, 159-184, 1916.
Siegel, C. L. "A Simple Proof of 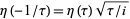 ." Mathematika 1, 4, 1954.
." Mathematika 1, 4, 1954.
Sloane, N. J. A. Sequences A010815, A091343, and A116397 in "The On-Line Encyclopedia of Integer Sequences."
Weber, H. Lehrbuch der Algebra, Vols. I-III. 1902. Reprinted as Lehrbuch der Algebra, Vols. I-III, 3rd rev ed. New York: Chelsea, 1979.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|