


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-6-2019
Date: 22-6-2019
Date: 19-5-2019
|

The modified bessel function of the second kind is the function 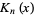 which is one of the solutions to the modified Bessel differential equation. The modified Bessel functions of the second kind are sometimes called the Basset functions, modified Bessel functions of the third kind (Spanier and Oldham 1987, p. 499), or Macdonald functions (Spanier and Oldham 1987, p. 499; Samko et al. 1993, p. 20). The modified Bessel function of the second kind is implemented in the Wolfram Language as BesselK[nu, z].
which is one of the solutions to the modified Bessel differential equation. The modified Bessel functions of the second kind are sometimes called the Basset functions, modified Bessel functions of the third kind (Spanier and Oldham 1987, p. 499), or Macdonald functions (Spanier and Oldham 1987, p. 499; Samko et al. 1993, p. 20). The modified Bessel function of the second kind is implemented in the Wolfram Language as BesselK[nu, z].
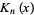 is closely related to the modified Bessel function of the first kind
is closely related to the modified Bessel function of the first kind 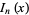 and Hankel function
and Hankel function 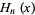 ,
,
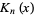 |
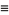 |
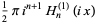 |
(1) |
 |
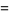 |
![1/2pii^(n+1)[J_n(ix)+iN_n(ix)]](http://mathworld.wolfram.com/images/equations/ModifiedBesselFunctionoftheSecondKind/Inline10.gif) |
(2) |
 |
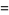 |
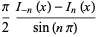 |
(3) |
(Watson 1966, p. 185). A sum formula for 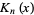 is
is
^k)/(k!(n+k)!),](http://mathworld.wolfram.com/images/equations/ModifiedBesselFunctionoftheSecondKind/NumberedEquation1.gif) |
(4) |
where 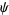 is the digamma function (Abramowitz and Stegun 1972). An integral formula is
is the digamma function (Abramowitz and Stegun 1972). An integral formula is
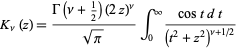 |
(5) |
which, for 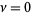 , simplifies to
, simplifies to
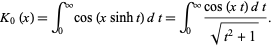 |
(6) |
Other identities are
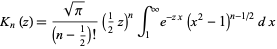 |
(7) |
for 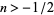 and
and
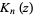 |
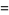 |
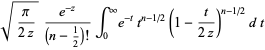 |
(8) |
 |
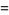 |
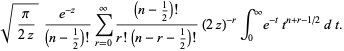 |
(9) |

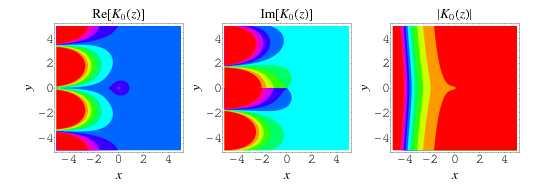
The special case of 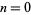 gives
gives 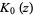 as the integrals
as the integrals
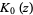 |
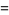 |
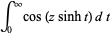 |
(10) |
 |
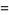 |
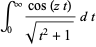 |
(11) |
(Abramowitz and Stegun 1972, p. 376).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Bessel Functions 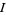 and
and 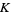 ." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.
." §9.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 374-377, 1972.
Arfken, G. "Modified Bessel Functions, 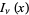 and
and 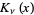 ." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
." §11.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 610-616, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Modified Bessel Functions of Integral Order" and "Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions." §6.6 and 6.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 229-245, 1992.
Samko, S. G.; Kilbas, A. A.; and Marichev, O. I. Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, p. 20, 1993.
Spanier, J. and Oldham, K. B. "The Basset 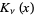 ." Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
." Ch. 51 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 499-507, 1987.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|