
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-7-2019
Date: 30-3-2019
Date: 30-3-2019
|
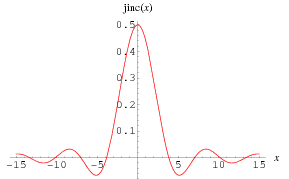
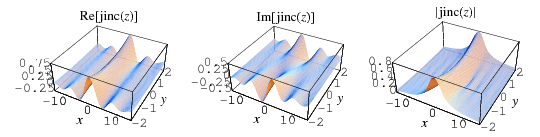
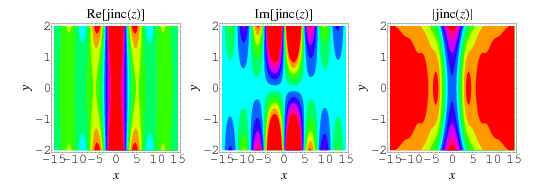
The jinc function is defined as
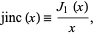 |
(1) |
where 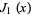 is a Bessel function of the first kind, and satisfies
is a Bessel function of the first kind, and satisfies 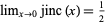 . The derivative of the jinc function is given by
. The derivative of the jinc function is given by
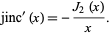 |
(2) |
The function is sometimes normalized by multiplying by a factor of 2 so that 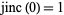 (Siegman 1986, p. 729).
(Siegman 1986, p. 729).
The first real inflection point of the function occurs when
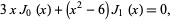 |
(3) |
namely 2.29991033... (OEIS A133920).
The unique real fixed point occurs at 0.48541702373... (OEIS A133921).
REFERENCES:
Bracewell, R. The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, p. 64, 1999.
Siegman, A. E. Lasers. Sausalito, CA: University Science Books, 1986.
Sloane, N. J. A. Sequences A133920 and A133921 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|