


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2019
Date: 2-5-2019
Date: 29-4-2018
|
The function defined by the contour integral
![J_(n,k)(z)
=1/(2pii)int^((0+))t^(-n-1)(t+1/t)^kexp[1/2z(t-1/t)]dt,](http://mathworld.wolfram.com/images/equations/BourgetFunction/NumberedEquation1.gif) |
where 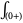 denotes the contour encircling the point
denotes the contour encircling the point 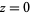 once in a counterclockwise direction. It is equal to
once in a counterclockwise direction. It is equal to
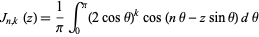 |
(Watson 1966, p. 326).
REFERENCES:
Bourget, J. "Mémoire sur les nombres de Cauchy et leur application à divers problèmes de mécanique céleste." J. de Math. 6, 33-54, 1861.
Giuliani, G. "Alcune osservazioni sopra le funzioni spheriche di ordine superiore al secondo e sopra altre funzioni che se ne possono dedurre (April, 1888)." Giornale di Mat. 26, 155-171, 1888.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, p. 465, 1988.
Watson, G. N. "The Functions of Bourget and Giuliani." §10.31 in A Treatise on the Theory of Bessel Functions, 2nd ed.Cambridge, England: Cambridge University Press, pp. 326-327, 1966.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|