Electron Penetration

The approximation in Equation (Si = 1) is a good first order description of electron shielding, but the actual Zeff experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in Zeff for different elements, as shown in Figure 1.1  for the elements of the first three rows of the periodic table.

Figure 1.1 : Relationship between the Effective Nuclear Charge Z_eff and the Atomic Number Z for the Outer Electrons of the Elements of the First Three Rows of the Periodic Table. Except for hydrogen, (Zeff is always less than Z, and (Zeff increases from left to right as you go across a row.

Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron's relative electron density (probability density) near the nucleus of an atom (Figure 1.2).

Electrons in different orbitals have different electron densities around the nucleus. In other words, penetration depends on the shell (n) and subshell (l). 

For example, a 1s electron (Figure 1.2 ; purple curve) has greater electron density near the nucleus than a 2p electron (Figure 1.2; red curve) and has a greater penetration. This related to the shielding constants since the 1s electrons are closer to the nucleus than a 2p electron, hence the 1s screens a 2p electron almost perfectly (S=1. However, the 2s electron has a lower shielding constant (S<1 because it can penetrate close to the nucleus in the small area of electron density within the first spherical node (Figure 1.2 ; green curve). In this way the 2s electron can "avoid" some of the shielding effect of the inner 1s electron.

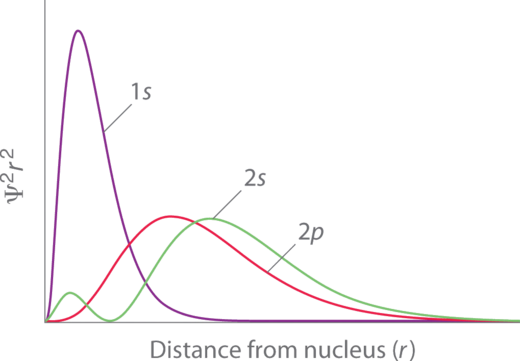
Figure 1.2

: Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of Zeff , which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.

For the same shell value (n) the penetrating power of an electron follows this trend in subshells (Figure 1.2): s>p>d≈f. for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend: