Jordan's Lemma

Jordan's lemma shows the value of the integral

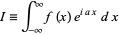(1)

along the infinite upper semicircle and with 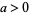 is 0 for "nice" functions which satisfy 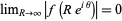. Thus, the integral along the real axis is just the sum of complex residues in the contour.

The lemma can be established using a contour integral 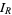 that satisfies

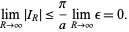(2)

To derive the lemma, write

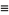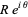			(3)
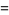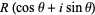			(4)
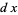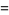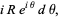			(5)

and define the contour integral

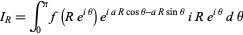(6)

Then

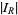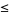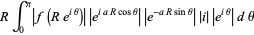			(7)
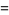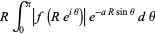			(8)
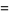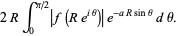			(9)

Now, if 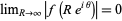, choose an  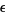such that 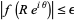, so

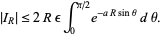(10)

But, for ,

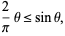(11)

so

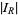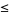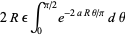			(12)
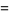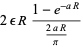			(13)
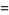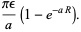			(14)

As long as 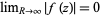, Jordan's lemma

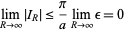(15)

then follows.

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 406-408, 1985.

Jordan, C. Cours d'Analyse de l'Ecole polytechnique, Tome 2, 3. éd., rev. et corrigé. Paris: Gauthier-Villars, pp. 285-86, 1909-1915.

Whittaker, E. T. and Watson, G. N. "Jordan's Lemma." §6.222 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 115-117, 1990.