


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 27-11-2018
Date: 11-12-2018
|
A relation connecting the values of a meromorphic function inside a disk with its boundary values on the circumference and with its zeros and poles (Jensen 1899, Levin 1980). Let 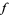 be holomorphic on a neighborhood of the closed disk
be holomorphic on a neighborhood of the closed disk 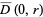 and
and 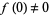 ,
, 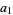 , ...,
, ..., 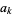 be the zeros of
be the zeros of 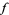 in the open disk
in the open disk 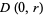 counted according to their multiplicities, and assume that
counted according to their multiplicities, and assume that 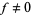 on
on 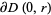 . Then
. Then
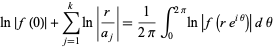 |
(Krantz 1999, p. 118).
REFERENCES:
Borwein, P. and Erdélyi, T. "Jensen's Formula." §4.2.E.10c in Polynomials and Polynomial Inequalities. New York: Springer-Verlag, p. 187, 1995.
Jensen, J. L. "Sur un nouvel et important théorème de la théorie des fonctions." Acta Math. 22, 359-364, 1899.
Krantz, S. G. "Jensen's Formula." §9.1.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 117-118, 1999.
Levin, B. Ya. Distribution of Zeros of Entire Functions. Providence, RI: Amer. Math. Soc., 1980.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|