
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 25-11-2018
Date: 14-10-2018
|
If a function analytic at the origin has no singularities other than poles for finite  , and if we can choose a sequence of contours
, and if we can choose a sequence of contours 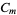 about
about 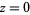 tending to infinity such that
tending to infinity such that 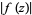 never exceeds a given quantity
never exceeds a given quantity 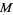 on any of these contours and
on any of these contours and 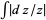 is uniformly bounded on them, then
is uniformly bounded on them, then
![f(z)=f(0)+lim[P_m(z)-P_m(0)],](http://mathworld.wolfram.com/images/equations/Mittag-LefflersTheorem/NumberedEquation1.gif) |
where 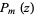 is the sum of the principal parts of
is the sum of the principal parts of 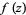 at all poles
at all poles 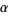 within
within 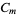 . If there is a pole at
. If there is a pole at 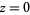 , then we can replace
, then we can replace 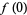 by the negative powers and the constant term in the Laurent series of
by the negative powers and the constant term in the Laurent series of 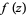 about
about 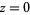 .
.
REFERENCES:
Jeffreys, H. and Jeffreys, B. S. "Mittag-Leffler's Theorem." §12.006 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 383-386, 1988.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ندوات وأنشطة قرآنية مختلفة يقيمها المجمَع العلمي في محافظتي النجف وكربلاء
|
|
|