


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-7-2019
Date: 23-6-2019
Date: 10-5-2018
|
There are many formulas of 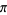 of many types. Among others, these include series, products, geometric constructions, limits, special values, and pi iterations.
of many types. Among others, these include series, products, geometric constructions, limits, special values, and pi iterations.
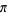 is intimately related to the properties of circles and spheres. For a circle of radius
is intimately related to the properties of circles and spheres. For a circle of radius 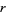 , the circumference and area are given by
, the circumference and area are given by
 |
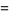 |
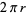 |
(1) |
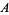 |
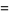 |
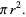 |
(2) |
Similarly, for a sphere of radius 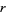 , the surface area and volume enclosed are
, the surface area and volume enclosed are
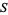 |
 |
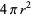 |
(3) |
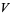 |
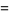 |
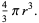 |
(4) |
An exact formula for 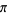 in terms of the inverse tangents of unit fractions is Machin's formula
in terms of the inverse tangents of unit fractions is Machin's formula
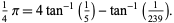 |
(5) |
There are three other Machin-like formulas, as well as thousands of other similar formulas having more terms.
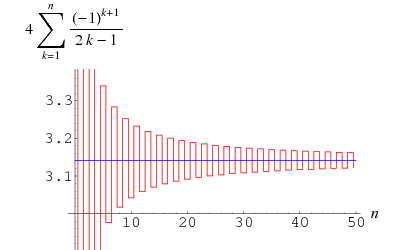
Gregory and Leibniz found
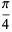 |
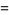 |
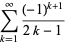 |
(6) |
 |
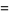 |
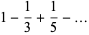 |
(7) |
(Wells 1986, p. 50), which is known as the Gregory series and may be obtained by plugging 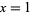 into the Leibniz series for
into the Leibniz series for 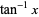 . The error after the
. The error after the 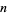 th term of this series in the Gregory series is larger than
th term of this series in the Gregory series is larger than 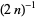 so this sum converges so slowly that 300 terms are not sufficient to calculate
so this sum converges so slowly that 300 terms are not sufficient to calculate 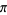 correctly to two decimal places! However, it can be transformed to
correctly to two decimal places! However, it can be transformed to
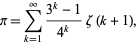 |
(8) |
where 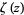 is the Riemann zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the error after
is the Riemann zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that the error after 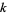 terms is
terms is 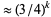 .
.
An infinite sum series to Abraham Sharp (ca. 1717) is given by
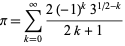 |
(9) |
(Smith 1953, p. 311). Additional simple series in which 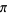 appears are
appears are
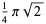 |
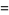 |
![sum_(k=1)^(infty)[((-1)^(k+1))/(4k-1)+((-1)^(k+1))/(4k-3)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline35.gif) |
(10) |
 |
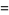 |
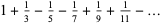 |
(11) |
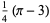 |
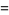 |
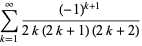 |
(12) |
 |
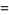 |
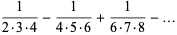 |
(13) |
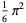 |
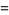 |
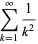 |
(14) |
 |
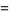 |
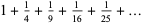 |
(15) |
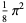 |
 |
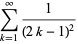 |
(16) |
 |
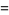 |
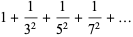 |
(17) |
(Wells 1986, p. 53).
In 1666, Newton used a geometric construction to derive the formula
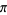 |
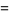 |
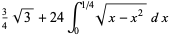 |
(18) |
 |
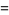 |
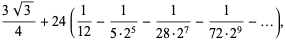 |
(19) |
which he used to compute 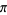 (Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be found from the integral
(Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be found from the integral
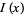 |
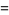 |
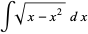 |
(20) |
 |
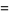 |
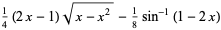 |
(21) |
by taking the series expansion of 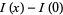 about 0, obtaining
about 0, obtaining
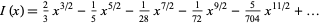 |
(22) |
(OEIS A054387 and A054388). Using Euler's convergence improvement transformation gives
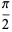 |
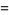 |
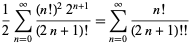 |
(23) |
 |
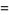 |
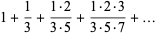 |
(24) |
 |
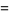 |
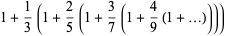 |
(25) |
(Beeler et al. 1972, Item 120).
This corresponds to plugging 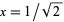 into the power series for the hypergeometric function
into the power series for the hypergeometric function 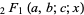 ,
,
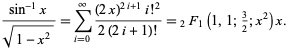 |
(26) |
Despite the convergence improvement, series (◇) converges at only one bit/term. At the cost of a square root, Gosper has noted that 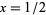 gives 2 bits/term,
gives 2 bits/term,
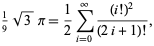 |
(27) |
and  gives almost 3.39 bits/term,
gives almost 3.39 bits/term,
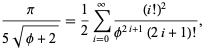 |
(28) |
where 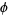 is the golden ratio. Gosper also obtained
is the golden ratio. Gosper also obtained
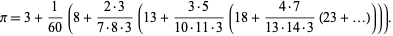 |
(29) |
A spigot algorithm for 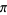 is given by Rabinowitz and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
is given by Rabinowitz and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
More amazingly still, a closed form expression giving a digit-extraction algorithm which produces digits of 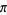 (or
(or 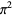 ) in base-16 was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
) in base-16 was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
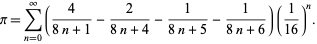 |
(30) |
This formula, known as the BBP formula, was discovered using the PSLQ algorithm (Ferguson et al. 1999) and is equivalent to
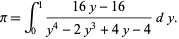 |
(31) |
There is a series of BBP-type formulas for 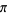 in powers of
in powers of 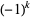 , the first few independent formulas of which are
, the first few independent formulas of which are
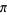 |
 |
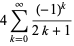 |
(32) |
 |
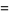 |
![3sum_(k=0)^(infty)(-1)^k[1/(6k+1)+1/(6k+5)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline95.gif) |
(33) |
 |
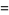 |
![4sum_(k=0)^(infty)(-1)^k[1/(10k+1)-1/(10k+3)+1/(10k+5)-1/(10k+7)+1/(10k+9)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline98.gif) |
(34) |
 |
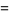 |
![sum_(k=0)^(infty)(-1)^k[3/(14k+1)-3/(14k+3)+3/(14k+5)+4/(14k+7)+4/(14k+9)-4/(14k+11)+4/(14k+13)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline101.gif) |
(35) |
 |
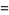 |
![sum_(k=0)^(infty)(-1)^k[2/(18k+1)+3/(18k+3)+2/(18k+5)-2/(18k+7)-2/(18k+11)+2/(18k+13)+3/(18k+15)+2/(18k+17)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline104.gif) |
(36) |
 |
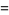 |
![sum_(k=0)^(infty)(-1)^k[3/(22k+1)-3/(22k+3)+3/(22k+5)-3/(22k+7)+3/(22k+9)+8/(22k+11)+3/(22k+13)-3/(22k+15)+3/(22k+17)-3/(22k+19)+1/(22k+21)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline107.gif) |
(37) |
Similarly, there are a series of BBP-type formulas for 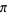 in powers of
in powers of 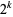 , the first few independent formulas of which are
, the first few independent formulas of which are
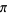 |
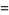 |
![sum_(k=0)^(infty)1/(16^k)[4/(8k+1)-2/(8k+4)-1/(8k+5)-1/(8k+6)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline112.gif) |
(38) |
 |
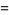 |
![1/2sum_(k=0)^(infty)1/(16^k)[8/(8k+2)+4/(8k+3)+4/(8k+4)-1/(8k+7)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline115.gif) |
(39) |
 |
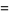 |
![1/(16)sum_(k=0)^(infty)1/(256^k)[(64)/(16k+1)-(32)/(16k+4)-(16)/(16k+5)-(16)/(16k+6)+4/(16k+9)-2/(16k+12)-1/(16k+13)-1/(16k+14)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline118.gif) |
(40) |
 |
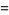 |
![1/(32)sum_(k=0)^(infty)1/(256^k)[(128)/(16k+2)+(64)/(16k+3)+(64)/(16k+4)-(16)/(16k+7)+8/(16k+10)+4/(16k+11)+4/(16k+12)-1/(16k+15)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline121.gif) |
(41) |
 |
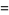 |
![1/(32)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(192)/(24k+3)-(256)/(24k+4)-(96)/(24k+6)-(96)/(24k+8)+(16)/(24k+10)-4/(24k+12)-3/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+20)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline124.gif) |
(42) |
 |
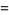 |
![1/(64)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(256)/(24k+2)-(384)/(24k+3)-(256)/(24k+4)-(64)/(24k+5)+(96)/(24k+8)+(64)/(24k+9)+(16)/(24k+10)+8/(24k+12)-4/(24k+13)+6/(24k+15)+6/(24k+16)+1/(24k+17)+1/(24k+18)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline127.gif) |
(43) |
 |
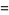 |
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(64)/(24k+3)+(128)/(24k+5)+(352)/(24k+6)+(64)/(24k+7)+(288)/(24k+8)+(128)/(24k+9)+(80)/(24k+10)+(20)/(24k+12)-(16)/(24k+14)-1/(24k+15)+6/(24k+16)-2/(24k+17)-1/(24k+19)+1/(24k+20)-2/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline130.gif) |
(44) |
 |
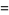 |
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(320)/(24k+3)+(256)/(24k+4)-(192)/(24k+5)-(224)/(24k+6)-(64)/(24k+7)-(192)/(24k+8)-(64)/(24k+9)-(64)/(24k+10)-(28)/(24k+12)-4/(24k+13)-5/(24k+15)+3/(24k+17)+1/(24k+18)+1/(24k+19)+1/(24k+21)-1/(24k+22)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline133.gif) |
(45) |
 |
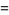 |
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(512)/(24k+1)-(256)/(24k+2)+(64)/(24k+3)-(512)/(24k+4)-(32)/(24k+6)+(64)/(24k+7)+(96)/(24k+8)+(64)/(24k+9)+(48)/(24k+10)-(12)/(24k+12)-8/(24k+13)-(16)/(24k+14)-1/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+19)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline136.gif) |
(46) |
 |
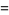 |
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(16384)/(32k+1)-(8192)/(32k+4)-(4096)/(32k+5)-(4096)/(32k+6)+(1024)/(32k+9)-(512)/(32k+12)-(256)/(32k+13)-(256)/(32k+14)+(64)/(32k+17)-(32)/(32k+20)-(16)/(32k+21)-(16)/(32k+22)+4/(32k+25)-2/(32k+28)-1/(32k+29)-1/(32k+30)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline139.gif) |
(47) |
 |
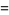 |
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(32768)/(32k+2)+(16384)/(32k+3)+(16384)/(32k+4)-(4096)/(32k+7)+(2048)/(32k+10)+(1024)/(32k+11)+(1024)/(32k+12)-(256)/(32k+15)+(128)/(32k+18)+(64)/(32k+19)+(64)/(32k+20)-(16)/(32k+23)+8/(32k+26)+4/(32k+27)+4/(32k+28)-1/(32k+31)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline142.gif) |
(48) |
F. Bellard found the rapidly converging BBP-type formula
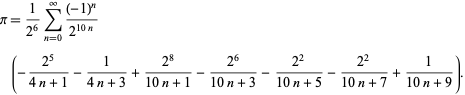 |
(49) |
A related integral is
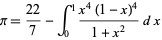 |
(50) |
(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, and Girgensohn 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). This integral was known by K. Mahler in the mid-1960s and appears in an exam at the University of Sydney in November 1960 (Borwein, Bailey, and Girgensohn, p. 3). Beukers (2000) and Boros and Moll (2004, p. 126) state that it is not clear if these exists a natural choice of rational polynomial whose integral between 0 and 1 produces 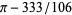 , where 333/106 is the next convergent. However, an integral exists for the fourth convergent, namely
, where 333/106 is the next convergent. However, an integral exists for the fourth convergent, namely
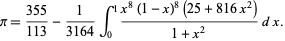 |
(51) |
(Lucas 2005; Bailey et al. 2007, p. 219). In fact, Lucas (2005) gives a few other such integrals.
Backhouse (1995) used the identity
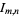 |
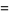 |
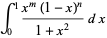 |
(52) |
 |
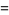 |
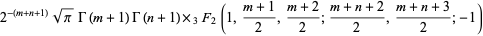 |
(53) |
 |
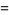 |
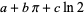 |
(54) |
for positive integer 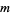 and
and 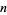 and where
and where 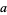 ,
, 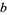 , and
, and 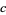 are rational constant to generate a number of formulas for
are rational constant to generate a number of formulas for 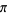 . In particular, if
. In particular, if 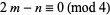 , then
, then 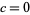 (Lucas 2005).
(Lucas 2005).
A similar formula was subsequently discovered by Ferguson, leading to a two-dimensional lattice of such formulas which can be generated by these two formulas given by
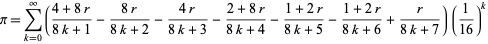 |
(55) |
for any complex value of 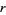 (Adamchik and Wagon), giving the BBP formula as the special case
(Adamchik and Wagon), giving the BBP formula as the special case 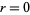 .
.
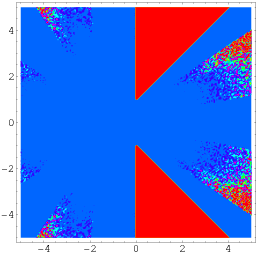
An even more general identity due to Wagon is given by
![pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)[(4(z+1)^(8k+1))/(8k+1)-(2(z+1)^(8k+4))/(8k+4)-((z+1)^(8k+5))/(8k+5)-((z+1)^(8k+6))/(8k+6)]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation15.gif) |
(56) |
(Borwein and Bailey 2003, p. 141), which holds over a region of the complex plane excluding two triangular portions symmetrically placed about the real axis, as illustrated above.
A perhaps even stranger general class of identities is given by
![pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)[8/((8k+1)_(2n))-4/((8k+3)_(2n))-4/((8k+4)_(2n))-2/((8k+5)_(2n))+1/((8k+7)_(2n))+1/((8k+8)_(2n))]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation16.gif) |
(57) |
which holds for any positive integer 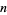 , where
, where 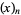 is a Pochhammer symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Even more amazingly, there is a closely analogous formula for the natural logarithm of 2.
is a Pochhammer symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Even more amazingly, there is a closely analogous formula for the natural logarithm of 2.
Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Borwein, Bailey, and Girgensohn (2004) have recently shown that 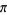 has no Machin-type BBP arctangent formula that is not binary, although this does not rule out a completely different scheme for digit-extraction algorithms in other bases.
has no Machin-type BBP arctangent formula that is not binary, although this does not rule out a completely different scheme for digit-extraction algorithms in other bases.
S. Plouffe has devised an algorithm to compute the 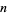 th digit of
th digit of 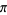 in any base in
in any base in 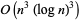 steps.
steps.
A slew of additional identities due to Ramanujan, Catalan, and Newton are given by Castellanos (1988ab, pp. 86-88), including several involving sums of Fibonacci numbers. Ramanujan found
![sum_(k=0)^infty((-1)^k(4k+1)[(2k-1)!!]^3)/([(2k)!!]^3)=sum_(k=0)^infty((-1)^k(4k+1)[Gamma(k+1/2)]^3)/(pi^(3/2)[Gamma(k+1)]^3)=2/pi](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation17.gif) |
(58) |
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) found the beautiful formula
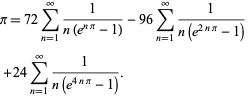 |
(59) |
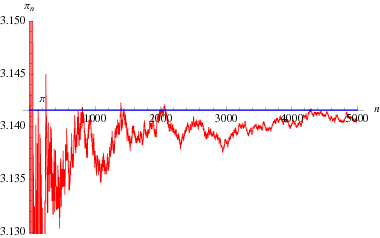
An interesting infinite product formula due to Euler which relates 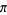 and the
and the 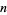 th prime
th prime 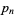 is
is
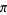 |
 |
![2/(product_(n=1)^(infty)[1+(sin(1/2pip_n))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline174.gif) |
(60) |
 |
 |
![2/(product_(n=2)^(infty)[1+((-1)^((p_n-1)/2))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline177.gif) |
(61) |
(Blatner 1997, p. 119), plotted above as a function of the number of terms in the product.
A method similar to Archimedes' can be used to estimate 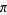 by starting with an
by starting with an 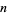 -gon and then relating the area of subsequent
-gon and then relating the area of subsequent 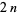 -gons. Let
-gons. Let 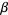 be the angle from the center of one of the polygon's segments,
be the angle from the center of one of the polygon's segments,
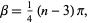 |
(62) |
then
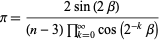 |
(63) |
(Beckmann 1989, pp. 92-94).
Vieta (1593) was the first to give an exact expression for 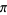 by taking
by taking 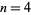 in the above expression, giving
in the above expression, giving
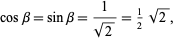 |
(64) |
which leads to an infinite product of nested radicals,
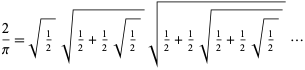 |
(65) |
(Wells 1986, p. 50; Beckmann 1989, p. 95). However, this expression was not rigorously proved to converge until Rudio in 1892.
A related formula is given by
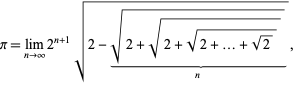 |
(66) |
which can be written
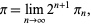 |
(67) |
where 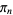 is defined using the iteration
is defined using the iteration
![pi_n=sqrt((1/2pi_(n-1))^2+[1-sqrt(1-(1/2pi_(n-1))^2)]^2)](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation25.gif) |
(68) |
with 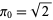 (J. Munkhammar, pers. comm., April 27, 2000). The formula
(J. Munkhammar, pers. comm., April 27, 2000). The formula
![pi=2lim_(m->infty)sum_(n=1)^msqrt([sqrt(1-((n-1)/m)^2)-sqrt(1-(n/m)^2)]^2+1/(m^2))](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation26.gif) |
(69) |
is also closely related.
A pretty formula for 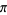 is given by
is given by
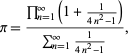 |
(70) |
where the numerator is a form of the Wallis formula for 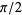 and the denominator is a telescoping sum with sum 1/2 since
and the denominator is a telescoping sum with sum 1/2 since
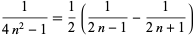 |
(71) |
(Sondow 1997).
A particular case of the Wallis formula gives
![pi/2=product_(n=1)^infty[((2n)^2)/((2n-1)(2n+1))]=(2·2)/(1·3)(4·4)/(3·5)(6·6)/(5·7)...](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation29.gif) |
(72) |
(Wells 1986, p. 50). This formula can also be written
![lim_(n->infty)(2^(4n))/(n(2n; n)^2)=pilim_(n->infty)(n[Gamma(n)]^2)/([Gamma(1/2+n)]^2)=pi,](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation30.gif) |
(73) |
where 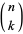 denotes a binomial coefficient and
denotes a binomial coefficient and 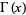 is the gamma function (Knopp 1990). Euler obtained
is the gamma function (Knopp 1990). Euler obtained
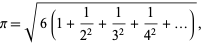 |
(74) |
which follows from the special value of the Riemann zeta function 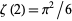 . Similar formulas follow from
. Similar formulas follow from 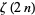 for all positive integers
for all positive integers 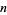 .
.
An infinite sum due to Ramanujan is
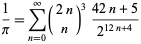 |
(75) |
(Borwein et al. 1989; Borwein and Bailey 2003, p. 109; Bailey et al. 2007, p. 44). Further sums are given in Ramanujan (1913-14),
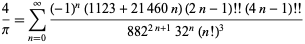 |
(76) |
and
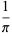 |
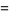 |
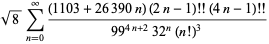 |
(77) |
 |
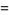 |
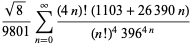 |
(78) |
(Beeler et al. 1972, Item 139; Borwein et al. 1989; Borwein and Bailey 2003, p. 108; Bailey et al. 2007, p. 44). Equation (78) is derived from a modular identity of order 58, although a first derivation was not presented prior to Borwein and Borwein (1987). The above series both give
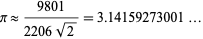 |
(79) |
(Wells 1986, p. 54) as the first approximation and provide, respectively, about 6 and 8 decimal places per term. Such series exist because of the rationality of various modular invariants.
The general form of the series is
!)/((3n)!(n!)^3)1/([j(t)]^n)=(sqrt(-j(t)))/pi,](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation35.gif) |
(80) |
where 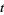 is a binary quadratic form discriminant,
is a binary quadratic form discriminant, 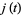 is the j-function,
is the j-function,
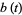 |
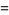 |
![sqrt(t[1728-j(t)])](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline203.gif) |
(81) |
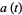 |
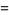 |
![(b(t))/6{1-(E_4(t))/(E_6(t))[E_2(t)-6/(pisqrt(t))]},](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline206.gif) |
(82) |
and the 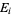 are Eisenstein series. A class number
are Eisenstein series. A class number 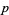 field involves
field involves 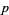 th degree algebraic integers of the constants
th degree algebraic integers of the constants 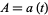 ,
, 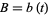 , and
, and 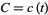 . Of all series consisting of only integer terms, the one gives the most numeric digits in the shortest period of time corresponds to the largest class number 1 discriminant of
. Of all series consisting of only integer terms, the one gives the most numeric digits in the shortest period of time corresponds to the largest class number 1 discriminant of 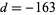 and was formulated by the Chudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that
and was formulated by the Chudnovsky brothers (1987). The 163 appearing here is the same one appearing in the fact that 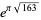 (the Ramanujan constant) is very nearly an integer. Similarly, the factor
(the Ramanujan constant) is very nearly an integer. Similarly, the factor 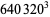 comes from the j-function identity for
comes from the j-function identity for 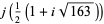 . The series is given by
. The series is given by
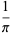 |
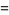 |
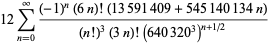 |
(83) |
 |
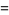 |
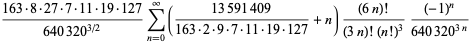 |
(84) |
(Borwein and Borwein 1993; Beck and Trott; Bailey et al. 2007, p. 44). This series gives 14 digits accurately per term. The same equation in another form was given by the Chudnovsky brothers (1987) and is used by the Wolfram Language to calculate 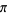 (Vardi 1991; Wolfram Research),
(Vardi 1991; Wolfram Research),
![pi=(426880sqrt(10005))/(A[_3F_2(1/6,1/2,5/6;1,1;B)-C_3F_2(7/6,3/2,(11)/6;2,2;B)]),](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation36.gif) |
(85) |
where
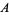 |
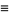 |
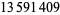 |
(86) |
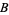 |
 |
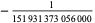 |
(87) |
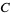 |
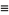 |
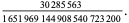 |
(88) |
The best formula for class number 2 (largest discriminant 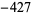 ) is
) is
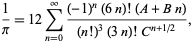 |
(89) |
where
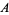 |
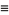 |
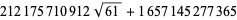 |
(90) |
 |
 |
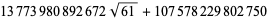 |
(91) |
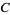 |
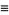 |
![[5280(236674+30303sqrt(61))]^3](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline242.gif) |
(92) |
(Borwein and Borwein 1993). This series adds about 25 digits for each additional term. The fastest converging series for class number 3 corresponds to 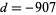 and gives 37-38 digits per term. The fastest converging class number 4 series corresponds to
and gives 37-38 digits per term. The fastest converging class number 4 series corresponds to 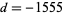 and is
and is
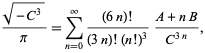 |
(93) |
where
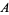 |
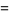 |
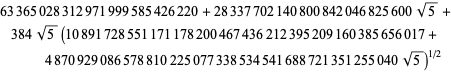 |
(94) |
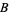 |
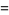 |
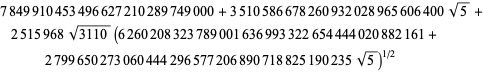 |
(95) |
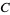 |
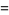 |
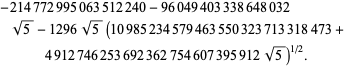 |
(96) |
This gives 50 digits per term. Borwein and Borwein (1993) have developed a general algorithm for generating such series for arbitrary class number.
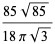
A complete listing of Ramanujan's series for 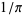 found in his second and third notebooks is given by Berndt (1994, pp. 352-354),
found in his second and third notebooks is given by Berndt (1994, pp. 352-354),
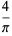 |
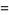 |
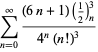 |
(97) |
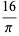 |
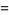 |
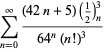 |
(98) |
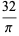 |
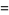 |
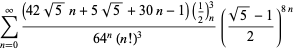 |
(99) |
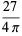 |
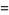 |
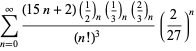 |
(100) |
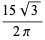 |
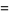 |
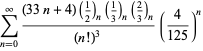 |
(101) |
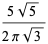 |
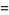 |
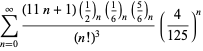 |
(102) |
 |
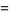 |
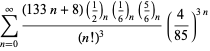 |
(103) |
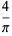 |
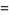 |
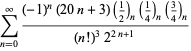 |
(104) |
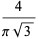 |
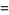 |
 |
(105) |
 |
 |
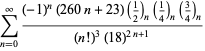 |
(106) |
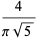 |
 |
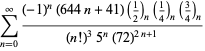 |
(107) |
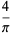 |
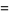 |
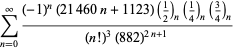 |
(108) |
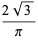 |
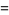 |
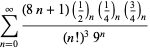 |
(109) |
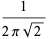 |
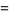 |
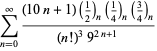 |
(110) |
 |
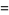 |
 |
(111) |
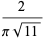 |
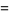 |
 |
(112) |
 |
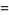 |
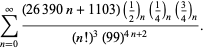 |
(113) |
These equations were first proved by Borwein and Borwein (1987a, pp. 177-187). Borwein and Borwein (1987b, 1988, 1993) proved other equations of this type, and Chudnovsky and Chudnovsky (1987) found similar equations for other transcendental constants (Bailey et al. 2007, pp. 44-45).
A complete list of independent known equations of this type is given by
 |
 |
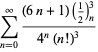 |
(114) |
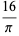 |
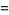 |
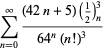 |
(115) |
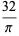 |
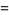 |
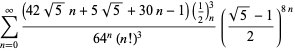 |
(116) |
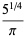 |
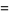 |
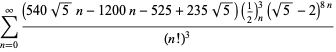 |
(117) |
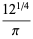 |
 |
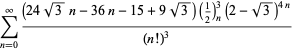 |
(118) |
for 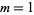 with nonalternating signs,
with nonalternating signs,
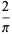 |
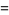 |
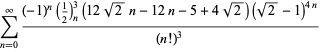 |
(119) |
 |
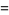 |
 |
(120) |
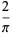 |
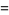 |
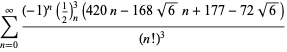 |
(121) |
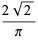 |
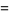 |
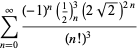 |
(122) |
for 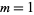 with alternating signs,
with alternating signs,
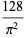 |
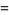 |
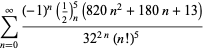 |
(123) |
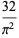 |
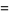 |
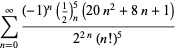 |
(124) |
for 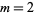 (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
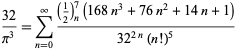 |
(125) |
for 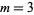 (Guillera 2002, 2003, 2006), and no others for
(Guillera 2002, 2003, 2006), and no others for 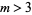 are known (Bailey et al. 2007, pp. 45-48).
are known (Bailey et al. 2007, pp. 45-48).
Bellard gives the exotic formula
![pi=1/(740025)[sum_(n=1)^infty(3P(n))/((7n; 2n)2^(n-1))-20379280],](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation40.gif) |
(126) |
where
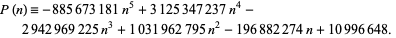 |
(127) |
Gasper quotes the result
![pi=(16)/3[lim_(x->infty)x_1F_2(1/2;2,3;-x^2)]^(-1),](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation42.gif) |
(128) |
where 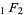 is a generalized hypergeometric function, and transforms it to
is a generalized hypergeometric function, and transforms it to
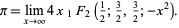 |
(129) |
A fascinating result due to Gosper is given by
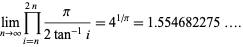 |
(130) |
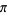 satisfies the inequality
satisfies the inequality
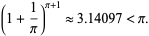 |
(131) |
D. Terr (pers. comm.) noted the curious identity
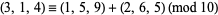 |
(132) |
involving the first 9 digits of pi.
REFERENCES:
Adamchik, V. and Wagon, S. "A Simple Formula for 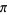 ." Amer. Math. Monthly 104, 852-855, 1997.
." Amer. Math. Monthly 104, 852-855, 1997.
Adamchik, V. and Wagon, S. "Pi: A 2000-Year Search Changes Direction." http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
Backhouse, N. "Note 79.36. Pancake Functions and Approximations to 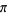 ." Math. Gaz. 79, 371-374, 1995.
." Math. Gaz. 79, 371-374, 1995.
Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 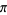 ,
, 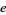 , and Euler's Constant." Math. Comput. 50, 275-281, 1988a.
, and Euler's Constant." Math. Comput. 50, 275-281, 1988a.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H.; Borwein, P.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Beck, G. and Trott, M. "Calculating Pi: From Antiquity to Moderns Times." http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html.
Beckmann, P. A History of Pi, 3rd ed. New York: Dorset Press, 1989.
Beeler, M. et al. Item 140 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Beukers, F. "A Rational Approximation to 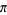 ." Nieuw Arch. Wisk. 5, 372-379, 2000.
." Nieuw Arch. Wisk. 5, 372-379, 2000.
Blatner, D. The Joy of Pi. New York: Walker, 1997.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987a.
Borwein, J. M. and Borwein, P. B. "Ramanujan's Rational and Algebraic Series for 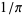 ." Indian J. Math. 51, 147-160, 1987b.
." Indian J. Math. 51, 147-160, 1987b.
Borwein, J. M. and Borwein, P. B. "More Ramanujan-Type Series for 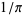 ." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
Borwein, J. M. and Borwein, P. B. "Class Number Three Ramanujan Type Series for 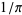 ." J. Comput. Appl. Math. 46, 281-290, 1993.
." J. Comput. Appl. Math. 46, 281-290, 1993.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi, or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Borwein, J. M.; Borwein, D.; and Galway, W. F. "Finding and Excluding 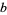 -ary Machin-Type Individual Digit Formulae." Canad. J. Math. 56, 897-925, 2004.
-ary Machin-Type Individual Digit Formulae." Canad. J. Math. 56, 897-925, 2004.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.
Chudnovsky, D. V. and Chudnovsky, G. V. "Approximations and Complex Multiplication According to Ramanujan." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987.
Dalzell, D. P. "On 22/7." J. London Math. Soc. 19, 133-134, 1944.
Dalzell, D. P. "On 22/7 and 355/113." Eureka 34, 10-13, 1971.
Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68, 351-369, 1999.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gasper, G. "Re: confluent pi." math-fun@cs.arizona.edu posting, Aug. 18, 1996.
Gosper, R. W. math-fun@cs.arizona.edu posting, Sept. 1996.
Gosper, R. W. "a product." math-fun@cs.arizona.edu posting, Sept. 27, 1996.
Gourdon, X. and Sebah, P. "Collection of Series for 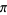 ." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
Guillera, J. "Some Binomial Series Obtained by the WZ-Method." Adv. Appl. Math. 29, 599-603, 2002.
Guillera, J. "About a New Kind of Ramanujan-Type Series." Exp. Math. 12, 507-510, 2003.
Guillera, J. "Generators of Some Ramanujan Formulas." Ramanujan J. 11, 41-48, 2006.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc. (Records of Proceedings at Meetings) 22, xii-xiii, 1924.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
Lucas, S. K. "Integral Proofs that 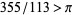 ." Austral. Math. Soc. Gaz. 32, 263-266, 2005.
." Austral. Math. Soc. Gaz. 32, 263-266, 2005.
MathPages. "Rounding Up to Pi." http://www.mathpages.com/home/kmath001.htm.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Rabinowitz, S. and Wagon, S. "A Spigot Algorithm for the Digits of 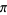 ." Amer. Math. Monthly 102, 195-203, 1995.
." Amer. Math. Monthly 102, 195-203, 1995.
Ramanujan, S. "Modular Equations and Approximations to 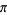 ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Sloane, N. J. A. Sequences A054387 and A054388 in "The On-Line Encyclopedia of Integer Sequences."
Smith, D. History of Mathematics, Vol. 2. New York: Dover, 1953.
Sondow, J. "Problem 88." Math Horizons, pp. 32 and 34, Sept. 1997.
Sondow, J. "A Faster Product for 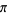 and a New Integral for
and a New Integral for 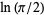 ." Amer. Math. Monthly 112, 729-734, 2005.
." Amer. Math. Monthly 112, 729-734, 2005.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Vieta, F. Uriorum de rebus mathematicis responsorum. Liber VII. 1593. Reprinted in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.
Wolfram Research, Inc. "Some Notes On Internal Implementation: Mathematical Constants." http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|