Schrödinger Equation

The Schrödinger equation describes the motion of particles in nonrelativistic quantum mechanics, and was first written down by Erwin Schrödinger. The time-dependent Schrödinger equation is given by

(1)

where 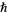 is the reduced Planck constant 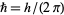,  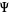is the time-dependent wavefunction,  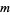is the mass of a particle,  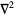is the Laplacian,  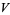is the potential, and  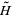is the Hamiltonian operator. The time-independent Schrödinger equation is

(2)

where 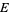 is the energy of the particle.

The one-dimensional versions of these equations are then

(3)

and

(4)

Variants of the one-dimensional Schrödinger equation have been considered in various contexts, including the following (where 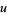 is a suitably non-dimensionalized version of the wavefunction). The logarithmic Schrödinger equation is given by

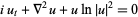(5)

(Cazenave 1983; Zwillinger 1997, p. 134), the nonlinear Schrödinger equation by

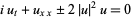(6)

(Calogero and Degasperis 1982, p. 56; Tabor 1989, p. 309; Zwillinger 1997, p. 134) or

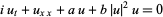(7)

(Infeld and Rowlands 2000, p. 126), and the derivative nonlinear Schrödinger equation by

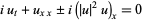(8)

(Calogero and Degasperis 1982, p. 56; Zwillinger 1997, p. 134).

REFERENCES:

Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, p. 56, 1982.

Cazenave, T. "Stable Solution of the Logarithmic Schrödinger Equation." Nonlinear Anal. 7, 1127-1140, 1983.

Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos, 2nd ed. Cambridge, England: Cambridge University Press, 2000.

Tabor, M. "The NLS Equation." §7.5.c in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, p. 309, 1989.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 134, 1997.