


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 23-7-2018
Date: 21-7-2018
|
The quantum electrodynamical law which applies to spin-1/2 particles and is the relativistic generalization of the Schrödinger equation. In 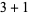 dimensions (three space dimensions and one time dimension), it is given by
dimensions (three space dimensions and one time dimension), it is given by
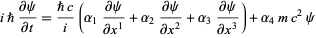 |
(1) |
(Bjorken and Drell 1964, p. 6), where 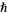 is h-bar,
is h-bar, 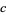 is the speed of light,
is the speed of light, 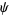 is the wavefunction,
is the wavefunction, 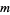 is the mass of the particle, and
is the mass of the particle, and 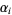 are the Dirac matrices (with
are the Dirac matrices (with 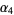 being called
being called 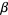 by Bjorken and Drell 1964, p. 8; Berestetskii et al. 1982, p. 78).
by Bjorken and Drell 1964, p. 8; Berestetskii et al. 1982, p. 78).
The Dirac equation can also be written in the concise form
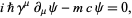 |
(2) |
(Griffiths 1987, p. 216), where
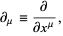 |
(3) |
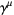 are Dirac matrices in the "Dirac basis" (Griffiths 1987, p. 216), and Einstein summation has been used to sum over
are Dirac matrices in the "Dirac basis" (Griffiths 1987, p. 216), and Einstein summation has been used to sum over 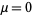 , 1, 2, 3.
, 1, 2, 3.
In 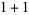 dimensions, a generalization of the Dirac equation is given by the system of partial differential equations
dimensions, a generalization of the Dirac equation is given by the system of partial differential equations
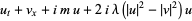 |
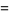 |
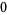 |
(4) |
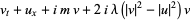 |
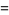 |
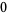 |
(5) |
(Alvarez et al. 1982; Zwillinger 1997, p. 137), where 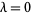 corresponds to the quantum electrodynamical equation.
corresponds to the quantum electrodynamical equation.
REFERENCES:
Alvarez, A.; Pen-Yu, K.; and Vazquez, L. "The Numerical Study of a Nonlinear One-Dimensional Dirac Equation." Appl. Math. Comput. 18, 1-15, 1983.
Berestetskii, V. B.; Lifshitz, E. M.; and Pitaevskii, L. P. Quantum Electrodynamics, 2nd ed. Oxford, England: Pergamon Press, 1982.
Bethe, H. A. and Salpeter, E. Quantum Mechanics of One- and Two-Electron Atoms. New York: Plenum, p. 37, 1977.
Bjorken, J. D. and Drell, S. D. "The Dirac Equation." §1.3 in Relativistic Quantum Mechanics. New York: McGraw-Hill, pp. 6-9, 1964.
Dirac, P. A. M. "The Quantum Theory of the Electron." Proc. Roy. Soc. London A117, 610-624, 1928.
Dirac, P. A. M. "The Quantum Theory of the Electron, Part II." Proc. Roy. Soc. London A118, 351-361, 1928.
Dirac, P. A. M. Principles of Quantum Mechanics, 4th ed. Oxford, England: Oxford University Press, 1982.
Griffiths, D. J. "The Dirac Equation" and "Solutions to the Dirac Equation." §7.1-7.2 in Introduction to Elementary Particles. New York: Wiley, pp. 213-222, 1987.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 137, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|