


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-5-2018
Date: 11-6-2018
Date: 5-7-2018
|
The second-order ordinary differential equation
 |
(1) |
is called Liouville's equation (Goldstein and Braun 1973; Zwillinger 1997, p. 124), as are the partial differential equations
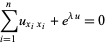 |
(2) |
(Matsumo 1987; Zwillinger 1997, p. 133) and
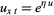 |
(3) |
(Calogero and Degasperis 1982, p. 60; Zwillinger 1997, p. 133).
REFERENCES:
Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, p. 60, 1982.
Goldstein, M. E. and Braun, W. H. Advanced Methods for the Solution of Differential Equations. NASA SP-316. Washington, DC: U.S. Government Printing Office, p. 98, 1973.
Matsumo, Y. "Exact Solution for the Nonlinear Klein-Gordon and Liouville Equations in Four-Dimensional Euclidean Space." J. Math. Phys. 28, 2317-2322, 1987.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 124 and 133, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|