
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2018
Date: 21-5-2018
Date: 30-5-2018
|
A linear ordinary differential equation of order 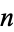 is said to be homogeneous if it is of the form
is said to be homogeneous if it is of the form
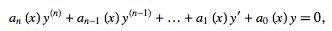 |
(1) |
where 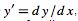 , i.e., if all the terms are proportional to a derivative of
, i.e., if all the terms are proportional to a derivative of 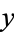 (or
(or 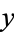 itself) and there is no term that contains a function of
itself) and there is no term that contains a function of 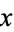 alone.
alone.
However, there is also another entirely different meaning for a first-order ordinary differential equation. Such an equation is said to be homogeneous if it can be written in the form
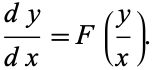 |
(2) |
Such equations can be solved in closed form by the change of variables 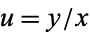 which transforms the equation into the separable equation
which transforms the equation into the separable equation
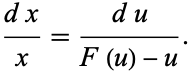 |
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 8th ed. New York: Wiley, pp. 49-50, 2004.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|