


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-12-2018
Date: 21-5-2018
Date: 3-7-2018
|
A natural extension of the Riemann p-differential equation given by
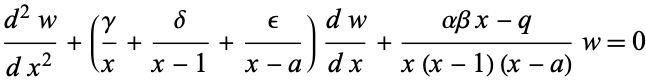 |
where
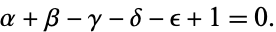 |
REFERENCES:
Decarreau, A.; Dumont-Lepage, M.-C.; Maroni, P.; Robert, A.; and Ronveaux, A. "Formes canoniques des équations confluentes de l'équation de Heun." Ann. Soc. Sci. de Bruxelles 92, 53-78, 1978.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 3. New York: Krieger, pp. 57-62, 1981.
Heun, K. "Zur Theorie der Riemann'schen Functionen Zweiter Ordnung mit Verzweigungspunkten." Math. Ann. 33, 161-179.
Ronveaux, A. (Ed.). Heun's Differential Equations. Oxford, England: Oxford University Press, 1995.
Slavyanov, S. Yu. and Lay, W. "The Heun Class of Equations." Ch. 3 in Special Functions: A Unified Theory Based on Singularities. Oxford, England: Oxford University Press, pp. 97-162, 2000.
Valent, G. "An Integral Transform Involving Heun Functions and a Related Eigenvalue Problem." SIAM J. Math. Anal. 17, 688-703, 1986.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, p. 576, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 123, 1997.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|