


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-6-2018
Date: 20-12-2018
Date: 3-7-2018
|
Consider a first-order ODE in the slightly different form
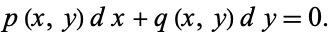 |
(1) |
Such an equation is said to be exact if
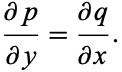 |
(2) |
This statement is equivalent to the requirement that a conservative field exists, so that a scalar potential can be defined. For an exact equation, the solution is
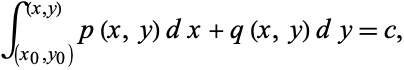 |
(3) |
where 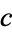 is a constant.
is a constant.
A first-order ODE (◇) is said to be inexact if
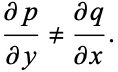 |
(4) |
For a nonexact equation, the solution may be obtained by defining an integrating factor 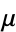 of (◇) so that the new equation
of (◇) so that the new equation
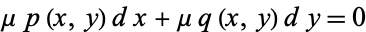 |
(5) |
satisfies
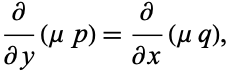 |
(6) |
or, written out explicitly,
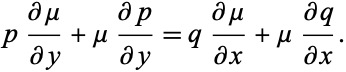 |
(7) |
This transforms the nonexact equation into an exact one. Solving (7) for 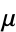 gives
gives
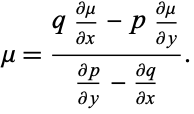 |
(8) |
Therefore, if a function 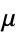 satisfying (8) can be found, then writing
satisfying (8) can be found, then writing
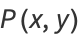 |
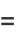 |
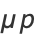 |
(9) |
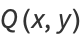 |
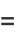 |
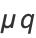 |
(10) |
in equation (◇) then gives
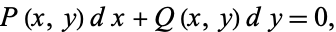 |
(11) |
which is then an exact ODE. Special cases in which 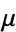 can be found include
can be found include 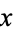 -dependent,
-dependent, 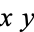 -dependent, and
-dependent, and 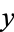 -dependent integrating factors.
-dependent integrating factors.
Given an inexact first-order ODE, we can also look for an integrating factor 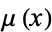 so that
so that
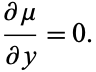 |
(12) |
For the equation to be exact in 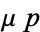 and
and 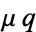 , the equation for a first-order nonexact ODE
, the equation for a first-order nonexact ODE
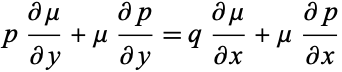 |
(13) |
becomes
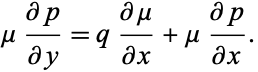 |
(14) |
Solving for 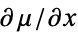 gives
gives
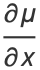 |
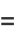 |
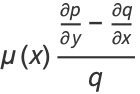 |
(15) |
 |
 |
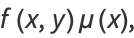 |
(16) |
which will be integrable if
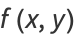 |
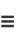 |
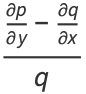 |
(17) |
 |
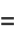 |
 |
(18) |
in which case
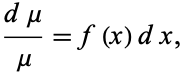 |
(19) |
so that the equation is integrable
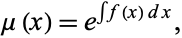 |
(20) |
and the equation
![[mup(x,y)]dx+[muq(x,y)]dy=0](http://mathworld.wolfram.com/images/equations/ExactFirst-OrderOrdinaryDifferentialEquation/NumberedEquation15.gif) |
(21) |
with known 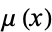 is now exact and can be solved as an exact ODE.
is now exact and can be solved as an exact ODE.
Given an exact first-order ODE, look for an integrating factor 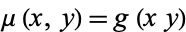 . Then
. Then
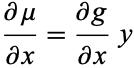 |
(22) |
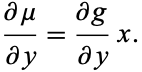 |
(23) |
Combining these two,
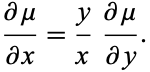 |
(24) |
For the equation to be exact in 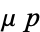 and
and 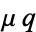 , the equation for a first-order nonexact ODE
, the equation for a first-order nonexact ODE
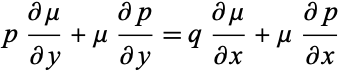 |
(25) |
becomes
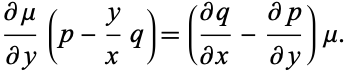 |
(26) |
Therefore,
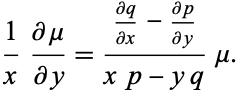 |
(27) |
Define a new variable
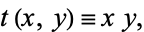 |
(28) |
then 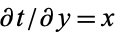 , so
, so
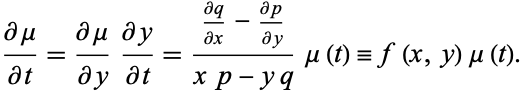 |
(29) |
Now, if
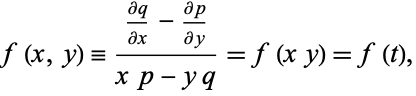 |
(30) |
then
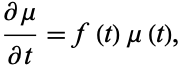 |
(31) |
so that
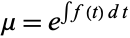 |
(32) |
and the equation
![[mup(x,y)]dx+[muq(x,y)]dy=0](http://mathworld.wolfram.com/images/equations/ExactFirst-OrderOrdinaryDifferentialEquation/NumberedEquation27.gif) |
(33) |
is now exact and can be solved as an exact ODE.
Given an inexact first-order ODE, assume there exists an integrating factor
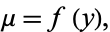 |
(34) |
so 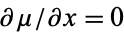 . For the equation to be exact in
. For the equation to be exact in 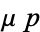 and
and 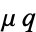 , equation (◇) becomes
, equation (◇) becomes
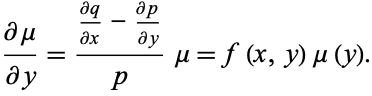 |
(35) |
Now, if
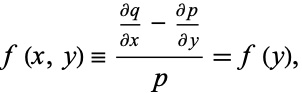 |
(36) |
then
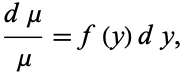 |
(37) |
so that
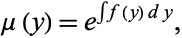 |
(38) |
and the equation
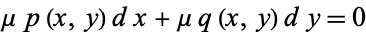 |
(39) |
is now exact and can be solved as an exact ODE.
Given a first-order ODE of the form
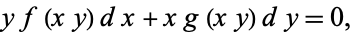 |
(40) |
define
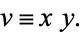 |
(41) |
Then the solution is
![{lnx=int(g(v)dv)/(c[g(v)-f(v)])+c for g(v)!=f(v); xy=c for g(v)=f(v).](http://mathworld.wolfram.com/images/equations/ExactFirst-OrderOrdinaryDifferentialEquation/NumberedEquation36.gif) |
(42) |
If
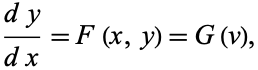 |
(43) |
where
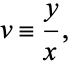 |
(44) |
then letting
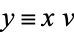 |
(45) |
gives
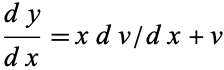 |
(46) |
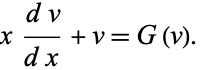 |
(47) |
This can be integrated by quadratures, so
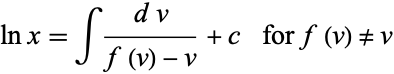 |
(48) |
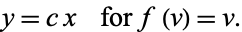 |
(49) |
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, 1986.
Ross, C. C. §3.3 in Differential Equations. New York: Springer-Verlag, 2004.
Zwillinger, D. Ch. 62 in Handbook of Differential Equations. San Diego, CA: Academic Press, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|