
تجربة توماس يانج
 المؤلف:
أمير أكزيل
المؤلف:
أمير أكزيل
 المصدر:
التعالق اكبر لغز في الفيزياء
المصدر:
التعالق اكبر لغز في الفيزياء
 الجزء والصفحة:
ص 29
الجزء والصفحة:
ص 29
 16-6-2016
16-6-2016
 13688
13688
تجربة توماس يانج
نحن نختار فحص ظاهرة (تجربة الثقب المزدوج) وهذه ظاهرة يستحيل، يستحيل تماما ، تفسيرها بأي وسيلة كلاسيكية، وتنطوي في داخلها علي لب ميكانيكا الكم. في الواقع، إنها تتضمن السر الوحيد. ريتشارد فيتمان Richard Feynman
كان توماس يانج Thomas Young (1773 -1829) البريطاني الجنسية، هو الفيزيائي الذي غيرت تجربته طريقة تفكيرنا في الضوء. في طفولته أبدي يانج عبقرية ملحوظة حينما تعلم القراءة في الثانية من عمره، وفي سن السادسة كان قد قرأ الكتاب المقدس مرتين وتعلم اللغة اللاتينية. وقبل أن يبلغ التاسعة عشرة كان يجيد ١٣ لغة، منها اليونانية والفرنسية والإيطالية، والعب، والكلدانية والسريانية والسومرية والفارسية والحبشية والعربية والتركية. وقام بدراسة حساب التفاضل والتكامل الذي وضعه نيوتن، وباقي مؤلفاته عن الميكانيكا والضوء، وكذلك كتاب لافوازييه عناصر الكيمياء Elements of Chemistry كما قرأ المسرحيات ودرس القانون وتعلم السياسة.
ومع نهاية القرن الثامن عشر درس يانج الطب في لندن وادنبرة وجوتنجر:، حيث نال شهادة الدكتوراه في الطب. وفي عام ١٧٩٤ ، اختير عضوا في الجمعية الملكية Royal Society وبعدها بثلاث سنوات، انتقل إلي جامعة كامبردج حيث نال شهادة دكتوراه ثانية وانضم إلي الكلية الملكية للأطباء. وعقب وفاة أحد أعمامه الأثرياء مخلفا له ميراثا يضم منزلا في لندن وأموالا كثيرة، نزح يانج إلي العاصمة وأسس بها عيادة طبية، لكنه لم يكن طبيبا ناجحا، ولذلك كرس جهوده للدراسة واجراء التجارب العلمية. ودرس يانج الإبصار وقدم لنا نظريته القائلة بأن العين تحتوي علي ثلاثة أنواع من مستقبلات الضوء للألوان الثلاثة الأساسية، وهي الأحمر والأزرق والأخضر. وأسهم يانج في الفلسفة الطبيعية، وفيزيولوجيا البصريات، وكان من أوائل من قاموا بالترجمة من الهيروغليفية المصرية. وتمثل أعظم إسهاماته للفيزياء في جهوده لتحوز النظرية الموجية للضوء القبول. وأجرى يانج تجربة الثقب المزدوج التي غدت شهيرة حاليا، لأنها تثبت ظاهرة التداخل من خلال النظرية الموجية.
وفي تجربته، وضع يانج مصدرا للضوء أمام حائل، وصنع ثقبين بالحائل لينفذ من خلالهما الضوء، ووضع شاشة خلف هذا الحائل، وعندما سلط يانج ضوء المصدر علي الحائل ذي الثقبين، حصل علي أحد أشكال تداخل الضوء interference
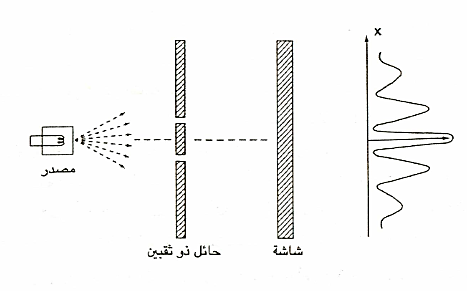
والمعلوم أن نموذج التداخل هو السمة المميزة للموجات. فالموجات بوسعها أن تتداخل مع بعضها البعض، وهو ما لا تفعله الجسيمات. أما ريتشارد فينمان فقد اعتبر أن النتيجة التي أسفرت عنها تجربة الثقب المزدوج ليانج- بالغة الأهمية، حتي إنه خصص معظم الفصل الأول من الجزء الثالث لمؤلفه الدراسي الشهير محاضرات فينمان في الفيزياء Feynman Lectures on Physics لهذا النوع من التجارب. وكان يعتقد أن نتيجة تجربة الشق المزدوج هي السر الرئيسي في ميكانيكا الكم . وشرح فينمان في كتابه فكرة تداخل الموجات في مقابل عدم تداخل الجسيمات باستخدام طلقات الرصاص. فلنفرض بندقية تطلق الرصاص عشوائيا علي حاجز ذي ثقبين ؟ نحصل علي النموذج الناتج الذي يوضحه الشكل التالي
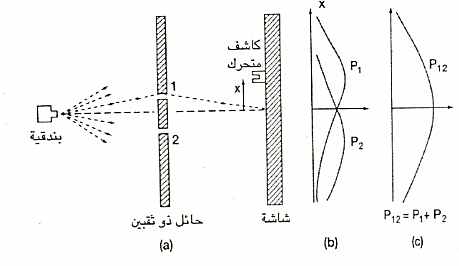
أما إذا مرت موجات الماء من خلال حاجز ذي ثقبين، فينتج الشكل التالي . هنا يحدث التداخل، مثلما يحدث في تجربة يانج باستخدام الضوء، بسبب أن لدينا موجبات كلاسيكية، إذ ربما تضاف سعتا موجتين لبعضهما ، ليسفر ذلك عن نشوء قمة علي الحائل، أو قد تتداخلان علي نحو هدام، لينتج قاع trough ، ولذلك تثبت تجربة يانج أن الضوء يتكون من موجات. لكن هل الضوء حقا موجة؟

مازالت الخاصية المزدوجة للضوء بين كونه موجة، وكونه تيارا من الجسيمات سمة مهمة للفيزياء حتي في القرن الواحد والعشرين. أما ميكانيكا الكم التي تم تطويرها في عشرينيات وثلاثينيات القرن العشرين، فإنها دعمت في الواقع الرأي القائل بأن الضوء يمتلك الخاصيتين الجسيمية والموجية علي حد سواء. وذكر لويس دي برولي Louis de Broglie الفيزيائي الفرنسي في عام ١٩٢٤ أنه حتي الأجسام الفيزيائية مثل الإلكترونات وغيرها من الجسيمات تمتلك الخواص الموجية. وأثبتت التجارب صحة وجهة نظره. وأثناء استنتاج ألبرت أينشتين في عام 1905 للتأثير الكهروضوئي، وضع أسس النظرية التي تنص علي أن الضوء يتكون من جسيمات، تماما علي غرار ما أكده نيوتن. وأصبح جسيم الضوء لدي أينشتين أخيرا يعرف باسم الفوتون، وهو الاسم المشتق من الكلمة اليونانية المقابلة للضوء. وطبقا لنظرية الكم، يمكن للضوء أن يتخذ كلا الشكلين: الموجة والجسيم، وهذه الازدواجية - المتناقضة ظاهريا - تعد دعامة أساسية في الفيزياء الحديثة. والأمر الملغز أن الضوء يتبدى في كلا المظهرين: الخصائص الموجية من تداخل وحيود، والخصائص الجسيمية، المتمثلة في تفاعل الجسيمات مع المادة. علي سبيل المثال فإن شعاعين من الضوء يتداخلان معا علي نحو يشابه إلي حد كبير موجتين صوتيتين تنبعثان من جهازي تكبير صوتي، وعلي الجانب الآخر، يتفاعل الضوء مع المادة بالطريقة نفسها التي تتم في حالة الجسيمات فقط، كما يحدث في حالة التأثير الكهروضوئي.
وقد أوضحت تجربة يانج أن الضوء يتكون من موجات، لكننا نعلم أيضا أن الضوء، علي نحو ما، عبارة عن جسيمات: فوتونات. وفي القرن العشرين، أعيد إجراء تجربة يانج باستخدام ضوء بالغ الضعف - الضوء الناتج كفوتون واحد في كل مرة - وبالتالي، لم يكن فن المحتمل علي الإطلاق وجود عدة فوتونات في جهاز التجربة في الوقت نفسه. الأمر المثير للذهول هو ظهور نموذج التداخل نفسه مع انقضاء الزمن الكافي حتي تتمكن الفوتونات في كل مرة من التراكم علي الشاشة. ما الذي كان يتداخل معه كل فوتون، إذا كان وحيدا في الجهاز التجريبي؟ يبدو أن الإجابة لابد أنها: يتداخل مع نفسه. بأحد المعاني، أن كل فوتون نفذ من الفتحتين، وليس من فتحة واحدة، وعند ظهوره علي الجانب الآخر، تداخل مع نفسه.
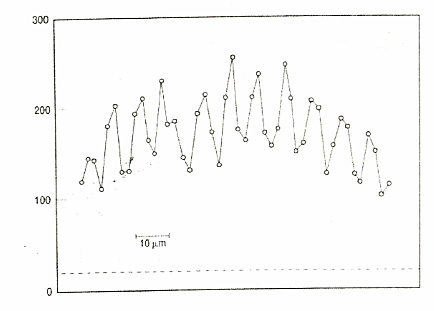
وتم إجراء تجربة يانج باستخدام الكثير من الكينونات التي نضعها في عداد الجسيمات: الإلكترونات منذ خمسينيات القرن العشرين، والنيوترونات في سبعينيات القرن العشرين، والذرات منذ الثمانينيات. وفي كل حالة: حدث نفس نموذج التداخل. هذه النتائج أثبتت مبدأ دي برولي، الذي يؤكد أن الجسيمات أيضا تبدي ظواهر موجية. وكمثال علي ذلك، في عام ١٩٨٩ ، أجري تونوميورا A. Tonomura وزملاؤه تجربة الشق المزدوج باستخدام الإلكترونات. والأشكال التالية توضح النتائج التي توصلوا إليها : وهي تبين بجلاء نموذج التداخل.

وقد توصل أنطون زايلنجر وزملاؤه إلي النموذج نفسه باستخدام النيوترونات التي تتحرك فقط بسرعة ٢ كيلو متر/ ثانية وذلك في عام1991. والشكل التالي يوضح نتائجهم.

وأمكن التوصل إلي نموذج مماثل باستخدام الذرات، وتبين من ذلك أن الخاصية الازدواجية بين الجسيمات والموجات تؤكد نفسها حتي للكينونات الأكبر.
وفي جامعة فيينا التي كان يعمل بها شرودنجر وماخ Mach تقدم أنطوان زايلنجر وزملاؤه خطوة أبعد، إذ زادوا من معرفتنا بالنظم الكمية لتشمل كينونات لم تكن لتندرج بالضرورة في عالم ما صغير جدا . (رغم أنه يتعين الإشارة إلي أن الفيزيائيين يعلمون أن بعض النظم كبيرة الحجم، مثل الموصلات الفائقة، يندرج سلوكها في إطار ميكانيكا الكم). والجدير بالذكر أن كرة الباكي bucky عبارة عن جزيء يتكون من 60 أو 70 ذرة كربون مرتبة في تركيب يماثل قبة جيوديسية مجوفة. واكتسبت هذه الكرات شهرتها من باكمنستر فولر Buckminster Fuller بعد إطلاق اسمه عليها . ويعد الجزيء الذي يتكون من 60 ذرة كينونة كبيرة نسبيا ، مقارنة بذرة واحدة، ومع هذا، ظهر نموذج التداخل الملغز نفسه عندما أجري زايلنجر وزملاؤه تجربتهم. والشكل التالي يوضح ترتيب التجربة.
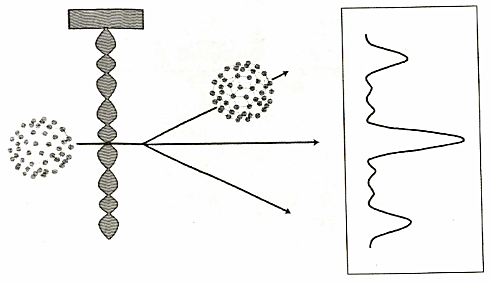
وفي كل حالة، نجد أن الجسيمات تصرفت كما لو أنها موجات. أيضا تم إجراء هذه التجارب علي جسيم واحد في كل مرة، وما زال نموذج التداخل باقيا . ما هو الشيء الذي كانت تتداخل معه هذه الجسيمات؟ الإجابة هي، بمعني ما، أن كل جسيم لم ينفذ من فتحة واحدة، لكن من الفتحتين معا ، وبالتالي فإن الجسيم يتداخل مع نفسه.
إن ما نشاهده هنا هو بيان جلي للمبدأ الكمي لتراكب الحالات. إذ ينص مبدأ التراكب علي أن حالة جديدة لنظام يمكن أن تتألف من حالتين أو أكثر، علي نحو يتيح للحالة الجديدة أن تشترك في بعض خصائص كل الحالات المتحدة. فإذا كانت A, B. تشيران إلي خاصيتين مختلفتين لجسيم، مثلا أن يكون في موضعين مختلفين، لذلك فإن تراكب الحالتين الذي يكتب علي الصورة A+B، ينطوي علي شيء مشترك سواء من الحالة A أو الحالة B. وعلي نحو خاص، فإن احتمالات الجسيم لاصفرية لأنه سيكون في حالة من الحالتين، وليس في مكان أخر، وذلك إذا تم رصد موضع الجسيم.
وفي حالة تجربة الشق المزدوج، فإن تجهيزات التجربة توفر للجسيم نوعا خاصا من التراكب: يكون الجسيم في الحالةA عندما يمر خلال الفتحةA، ويكون في الحالة B عندما يمر من الفتحة B. ويكون تراكب الحالتين هو توليف لـجسيم ينفذ من الفتحة "A مع جسيم ينفذ من الفتحة ."B ويتحد المساران، ويكون هناك بالتالي احتمالان غير صفريين، إذا أمكن ملاحظة الجسيمين، وبفرض إمكان ملاحظة الجسيم وهو ينفذ من خلال تجهيزات التجربة، تغدو فرصة رصده 50% مارا من الفتحة A وكذلك، 50% وهو يمر من الفتحة B . لكن إذا لم تتم ملاحظة الجسيم أثناء مروره في تجهيزات التجربة، بل تم ذلك فقط في نهايتها وهو يتجمع ملي الشاشة، فإن التراكب ينطبق خلالها حتي النهاية؟ بمعني، أن الجسيم مر من كلا الفتحتين، وما أن وصل إلي نهاية تجهيزات التجربة تداخل مع نفسه. إن تراكب الحالتين هو اللغز الأكبر في ميكانيكا الكم. وينطوي مبدأ التراكب في داخله علي فكرة التعالق.
 الاكثر قراءة في تجارب فيزيائية
الاكثر قراءة في تجارب فيزيائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


