Spin
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص308-309
2025-11-23
40
Spin
Stern and Gerlach observed two bands of Ag atoms in their experiment. This observation seems to conflict with one of the predictions of quantum mechanics, because an angular momentum l gives rise to 2l + 1 orientations, which is equal to 2 only if l = 1/2, contrary to the conclusion that l must be an integer. The conflict was resolved by the suggestion that the angular momentum they were observing was not due to orbital angular momentum (the motion of an electron around the atomic nucleus) but arose instead from the motion of the electron about its own axis. This intrinsic angular momentum of the electron is called its spin. The explanation of the existence of spin emerged when Dirac combined quantum mechanics with special relativity and estab-lished the theory of relativistic quantum mechanics. The spin of an electron about its own axis does not have to satisfy the same bound ary conditions as those for a particle circulating around a central point, so the quantum number for spin angular momentum is subject to different restrictions. To distinguish this spin angular momentum from orbital angular momentum we use the spin quantum number s (in place of l; like l, s is a non-negative number) and ms, the spin magnetic quantum number, for the projection on the z-axis. The magnitude of the spin angular momentum is {s(s + 1)}1/2h and the component msh is restricted to the 2s + 1 values
ms =s, s −1,..., −s
The detailed analysis of the spin of a particle is sophisticated and shows that the property should not be taken to be an actual spinning motion. It is better to regard ‘spin’ as an intrinsic property like mass and charge. However, the picture of an actual spinning motion can be very useful when used with care. For an electron it turns out that only one value of s is allowed, namely s = 1–2, corresponding to an angular momentum of magnitude (3/4)1/2h = 0.866$. This spin angular momentum is an intrinsic property of the electron, like its rest mass and its charge, and every electron has exactly the same value: the magnitude of the spin angular momentum of an electron cannot be changed. The spin may lie in 2s + 1 = 2 different orientations (Fig. 9.41).
One orientation corresponds to ms =+1/2 (this state is often denoted α or ↑); the other orientation corresponds to ms =−1/2 (this state is denoted β or ↓). The outcome of the Stern–Gerlach experiment can now be explained if we suppose that each Ag atom possesses an angular momentum due to the spin of a single electron, because the two bands of atoms then correspond to the two spin orientations. Why the atoms behave like this is explained in Chapter 10 (but it is already probably familiar from introductory chemistry that the ground-state configuration of a silver atom is [Kr]4d105s1, a single unpaired electron outside a closed shell). Like the electron, other elementary particles have characteristic spin. For example, protons and neutrons are spin-1/2 particles (that is, s = 1/2) and invariably spin with angular momentum (3/4)1/2h = 0.866$. Because the masses of a proton and a neutron are so much greater than the mass of an electron, yet they all have the same spin angular momentum, the classical picture would be of these two particles spinning much more slowly than an electron. Some elementary particles have s = 1, and so have an intrinsic angular momentum of magnitude 2 1/2h. Some mesons are spin-1 particles (as are some atomic nuclei), but for our purposes the most important spin-1 particle is the photon. From the discussion in this chapter, we see that the photon has zero rest mass, zero charge, an energy hν, a linear momentum h/λ or hν/c, an intrinsic angular momentum of 2 1/2h, and travels at the speed c. We shall see the importance of photon spin in the next chapter. Particles with half-integral spin are called fermions and those with integral spin (including 0) are called bosons. Thus, electrons and protons are fermions and pho tons are bosons. It is a very deep feature of nature that all the elementary particles that constitute matter are fermions whereas the elementary particles that are responsible for the forces that bind fermions together are all bosons. Photons, for example, transmit the electromagnetic force that binds together electrically charged particles. Matter, therefore, is an assembly of fermions held together by forces conveyed by bosons. The properties of angular momentum that we have developed are set out in Table 9.4. As mentioned there, when we use the quantum numbers l and ml we shall mean orbital angular momentum (circulation in space). When we use s and ms we shall mean spin angular momentum (intrinsic angular momentum). When we use j and mj we shall mean either (or, in some contexts to be described in Chapter 10, a combination of orbital and spin momenta).
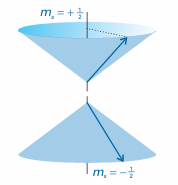
Fig. 9.41 An electron spin (s = 1/2) can take only two orientations with respect to a specified axis. An α electron (top) is an electron with ms =+1/2; a β electron (bottom) is an electron with ms=-1/2 The vector representing the spin angular momentum lies at an angle of 55° to the z-axis (more precisely, the half-angle of the cones is arccos (1/3 1/2)).
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
