The Nernst equation
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص219-221
2025-11-18
38
The Nernst equation
A cell in which the overall cell reaction has not reached chemical equilibrium can do electrical work as the reaction drives electrons through an external circuit. The work that a given transfer of electrons can accomplish depends on the potential difference between the two electrodes. This potential difference is called the cell potential and is measured in volts, V (1 V = 1 J C−1s). When the cell potential is large, a given number of electrons travelling between the electrodes can do a large amount of electrical work. When the cell potential is small, the same number of electrons can do only a small amount of work. A cell in which the overall reaction is at equilibrium can do no work, and then the cell potential is zero. According to the discussion in Section 3.5e, we know that the maximum non expansion work, which in the current context is electrical work, that a system (the cell) can do is given by eqn 3.38 (we,max =∆G), with ∆G identified (as we shall show) with the Gibbs energy of the cell reaction, ∆rG. It follows that, to draw thermodynamic conclusions from measurements of the work a cell can do, we must ensure that the cell is operating reversibly, for only then is it producing maximum work. Moreover, we saw in Section 7.1a that the reaction Gibbs energy is actually a property relating to a specified composition of the reaction mixture. Therefore, to make use of ∆rG we must ensure that the cell is operating reversibly at a specific, constant composition. Both these conditions are achieved by measuring the cell potential when it is balanced by an exactly opposing source of potential so that the cell reaction occurs reversibly, the composition is constant, and no current flows: in effect, the cell reaction is poised for change, but not actually changing. The resulting potential difference is called the electromotive force (emf), E, of the cell. As we show in the Justification below, the relation between the reaction Gibbs energy and the emf of the cell is , −νFE=∆rG , where F is Faraday’s constant, F = eNA, and ν is the stoichiometric coefficient of the electrons in the half-reactions into which the cell reaction can be divided. This equation is the key connection between electrical measurements on the one hand and thermodynamic properties on the other. It will be the basis of all that follows.
Justification 7.3 The relation between the electromotive force and the reaction Gibbs energy We consider the change in G when the cell reaction advances by an infinitesimal amount dξ at some composition. From eqn 7.15 we can write (at constant temper ature and pressure) , dG=∆rGdξ , The maximum non-expansion (electrical) work that the reaction can do as it advances by dξ at constant temperature and pressure is therefore , dwe =∆rGdξ , This work is infinitesimal, and the composition of the system is virtually constant when it occurs.
Suppose that the reaction advances by dξ, then νdξ electrons must travel from the anode to the cathode. The total charge transported between the electrodes when this change occurs is −νeNAdξ (because νdξ is the amount of electrons and the charge per mole of electrons is −eNA). Hence, the total charge transported is −νFdξ because eNA = F. The work done when an infinitesimal charge −νFdξ travels from the anode to the cathode is equal to the product of the charge and the potential difference E (see Table 2.1 and Appendix 3): dwe =−νFEdξ , When we equate this relation to the one above (dwe =∆rGdξ), the advancement dξ cancels, and we obtain eqn 7.27.
It follows from eqn 7.27 that, by knowing the reaction Gibbs energy at a specified composition, we can state the cell emf at that composition. Note that a negative reaction Gibbs energy, corresponding to a spontaneous cell reaction, corresponds to a positive cell emf. Another way of looking at the content of eqn 7.27 is that it shows that the driving power of a cell (that is, its emf) is proportional to the slope of the Gibbs energy with respect to the extent of reaction. It is plausible that a reaction that is far from equilibrium (when the slope is steep) has a strong tendency to drive electrons through an external circuit (Fig. 7.14). When the slope is close to zero (when the cell reaction is close to equilibrium), the emf is small.
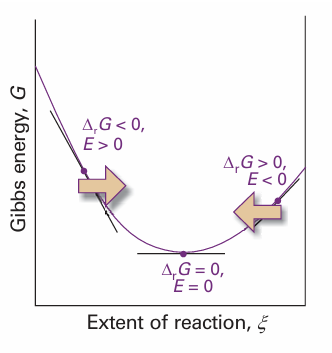
Fig. 7.14 A spontaneous reaction occurs in the direction of decreasing Gibbs energy. When expressed in terms of a cell potential, the spontaneous direction of change can be expressed in terms of the cell emf, E. The reaction is spontaneous as written (from left to right on the illustration) when E>0. The reverse reaction is spontaneous when E<0 When the cell reaction is at equilibrium, the cell potential is zero.
We can go on to relate the emf to the activities of the participants in the cell reaction. We know that the reaction Gibbs energy is related to the composition of the reaction mixture by eqn 7.11 (∆rG =∆rGo + RT ln Q); it follows, on division of both sides by −νF, that
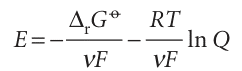
The first term on the right is written
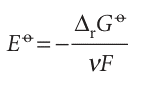
and called the standard emf of the cell. That is, the standard emf is the standard reaction Gibbs energy expressed as a potential (in volts). It follows that
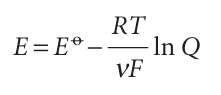
This equation for the emf in terms of the composition is called the Nernst equation; the dependence of cell potential on composition that it predicts is summarized in Fig. 7.15. One important application of the Nernst equation is to the determination of the pH of a solution and, with a suitable choice of electrodes, of the concentration of other ions (Section 7.9c). We see from eqn 7.29 that the standard emf (which will shortly move to centre stage of the exposition) can be interpreted as the emf when all the reactants and products in the cell reaction are in their standard states, for then all activities are 1, so Q = 1 and ln Q = 0. However, the fact that the standard emf is merely a disguised form of the standard reaction Gibbs energy (eqn 7.28) should always be kept in mind and under lies all its applications.
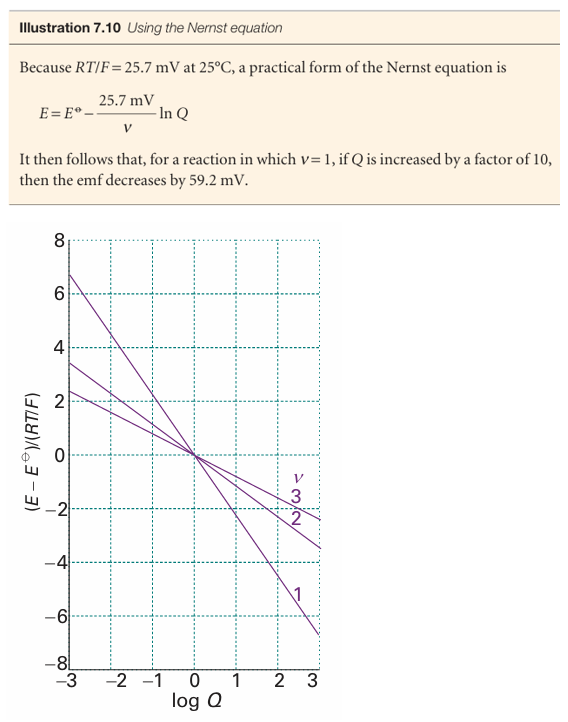
Fig. 7.15 The variation of cell emf with the value of the reaction quotient for the cell reaction for different values of ν (the number of electrons transferred). At 298 K, RT/F =25.69 mV, so the vertical scale refers to multiples of this value.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
