In checking out whether the contraction idea is in harmony with the facts in other experiments, it turns out that everything is correct provided that the times are also modified, in the manner expressed in the fourth equation of the set (15.3). That is because the time 2t₃, calculated for the trip from B to C and back, is not the same when calculated by a man performing the experiment in a moving space ship as when calculated by a stationary observer who is watching the space ship. To the man in the ship the time is simply 2L/c, but to the other observer it is (Eq. 15.5). In other words, when the outsider sees the man in the space ship lighting a cigar, all the actions appear to be slower than normal, while to the man inside, everything moves at a normal rate. So not only must the lengths shorten, but also the time-measuring instruments (“clocks”) must apparently slow down. That is, when the clock in the space ship records 1 second elapsed, as seen by the man in the ship, it shows second to the man outside.

This slowing of the clocks in a moving system is a very peculiar phenomenon, and is worth an explanation. In order to understand this, we have to watch the machinery of the clock and see what happens when it is moving. Since that is rather difficult, we shall take a very simple kind of clock. The one we choose is rather a silly kind of clock, but it will work in principle: it is a rod (meter stick) with a mirror at each end, and when we start a light signal between the mirrors, the light keeps going up and down, making a click every time it comes down, like a standard ticking clock. We build two such clocks, with exactly the same lengths, and synchronize them by starting them together; then they agree always thereafter, because they are the same in length, and light always travels with speed c. We give one of these clocks to the man to take along in his space ship, and he mounts the rod perpendicular to the direction of motion of the ship; then the length of the rod will not change. How do we know that perpendicular lengths do not change? The men can agree to make marks on each other’s y-meter stick as they pass each other. By symmetry, the two marks must come at the same y- and y′-coordinates, since otherwise, when they get together to compare results, one mark will be above or below the other, and so we could tell who was really moving.

Fig. 15–3. (a) A “light clock” at rest in the S′ system. (b) The same clock, moving through the S system. (c) Illustration of the diagonal path taken by the light beam in a moving “light clock.”

Now let us see what happens to the moving clock. Before the man took it aboard, he agreed that it was a nice, standard clock, and when he goes along in the space ship, he will not see anything peculiar. If he did, he would know he was moving—if anything at all changed because of the motion, he could tell he was moving. But the principle of relativity says this is impossible in a uniformly moving system, so nothing has changed. On the other hand, when the external observer looks at the clock going by, he sees that the light, in going from mirror to mirror, is “really” taking a zigzag path, since the rod is moving sidewise all the while. We have already analyzed such a zigzag motion in connection with the Michelson-Morley experiment. If in a given time the rod moves forward a distance proportional to u in Fig. 15–3, the distance the light travels in the same time is proportional to c, and the vertical distance is therefore proportional to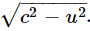

That is, it takes a longer time for light to go from end to end in the moving clock than in the stationary clock. Therefore, the apparent time between clicks is longer for the moving clock, in the same proportion as shown in the hypotenuse of the triangle (that is the source of the square root expressions in our equations). From the figure it is also apparent that the greater u is, the more slowly the moving clock appears to run. Not only does this particular kind of clock run more slowly, but if the theory of relativity is correct, any other clock, operating on any principle whatsoever, would also appear to run slower, and in the same proportion—we can say this without further analysis. Why is this so?

To answer the above question, suppose we had two other clocks made exactly alike with wheels and gears, or perhaps based on radioactive decay, or something else. Then we adjust these clocks so they both run in precise synchronism with our first clocks. When light goes up and back in the first clocks and announces its arrival with a click, the new models also complete some sort of cycle, which they simultaneously announce by some doubly coincident flash, or bong, or other signal. One of these clocks is taken into the space ship, along with the first kind. Perhaps this clock will not run slower, but will continue to keep the same time as its stationary counterpart, and thus disagree with the other moving clock. Ah no, if that should happen, the man in the ship could use this mismatch between his two clocks to determine the speed of his ship, which we have been supposing is impossible. We need not know anything about the machinery of the new clock that might cause the effect—we simply know that whatever the reason, it will appear to run slow, just like the first one.

Now if all moving clocks run slower, if no way of measuring time gives anything but a slower rate, we shall just have to say, in a certain sense, that time itself appears to be slower in a space ship. All the phenomena there—the man’s pulse rate, his thought processes, the time he takes to light a cigar, how long it takes to grow up and get old—all these things must be slowed down in the same proportion, because he cannot tell he is moving. The biologists and medical men sometimes say it is not quite certain that the time it takes for a cancer to develop will be longer in a space ship, but from the viewpoint of a modern physicist it is nearly certain; otherwise, one could use the rate of cancer development to determine the speed of the ship!

A very interesting example of the slowing of time with motion is furnished by muons, which are particles that disintegrate spontaneously after an average lifetime of 2.2×10⁻⁶ sec. They come to the earth in cosmic rays, and can also be produced artificially in the laboratory. Some of them disintegrate in midair, but the remainder disintegrate only after they encounter a piece of material and stop. It is clear that in its short lifetime a muon cannot travel, even at the speed of light, much more than 600 meters. But although the muons are created at the top of the atmosphere, some 10 kilometers up, yet they are actually found in a laboratory down here, in cosmic rays. How can that be? The answer is that different muons move at various speeds, some of which are very close to the speed of light. While from their own point of view they live only about 2μsec, from our point of view they live considerably longer—enough longer that they may reach the earth. The factor by which the time is increased has already been given as The average life has been measured quite accurately for muons of different velocities, and the values agree closely with the formula.

We do not know why the muon disintegrates or what its machinery is, but we do know its behavior satisfies the principle of relativity. That is the utility of the principle of relativity—it permits us to make predictions, even about things that otherwise we do not know much about. For example, before we have any idea at all about what makes the muon disintegrate, we can still predict that when it is moving at nine-tenths of the speed of light, the apparent length of time that it lasts is sec; and our prediction works—that is the good thing about it.

مواضيع ذات صلة

Relativistic energy

Relativistic mass

Transformation of velocities

The twin paradox

Equivalence of mass and energy

Relativistic dynamics

The Lorentz contraction

The Michelson-Morley experiment

نظرية المفعول الكهروضوئي ونقد معادلة ط = ك × سر2 للعالم حسن كامل الصباح:

معادلة أينشتاين جامدة المضمون

تاريخ المعادلة المشهورة الطاقة = الكتلة × مربع سرعة الضوء ط = ك × سر2

النسبية الخاصة.. نظرية بوانكاريه