First of all, Kepler found that each planet goes around the sun in a curve called an ellipse, with the sun at a focus of the ellipse. An ellipse is not just an oval, but is a very specific and precise curve that can be obtained by using two tacks, one at each focus, a loop of string, and a pencil; more mathematically, it is the locus of all points the sum of whose distances from two fixed points (the foci) is a constant. Or, if you will, it is a foreshortened circle (Fig. 7–1).

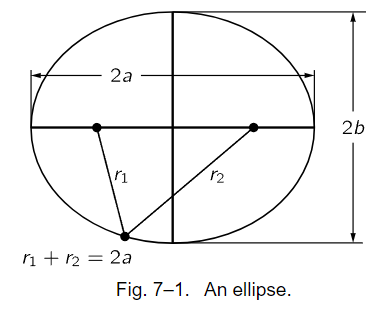
Fig. 7–1. An ellipse.

Kepler’s second observation was that the planets do not go around the sun at a uniform speed, but move faster when they are nearer the sun and more slowly when they are farther from the sun, in precisely this way: Suppose a planet is observed at any two successive times, let us say a week apart, and that the radius vector ¹ is drawn to the planet for each observed position. The orbital arc traversed by the planet during the week, and the two radius vectors, bound a certain plane area, the shaded area shown in Fig. 7–2. If two similar observations are made a week apart, at a part of the orbit farther from the sun (where the planet moves more slowly), the similarly bounded area is exactly the same as in the first case. So, in accordance with the second law, the orbital speed of each planet is such that the radius “sweeps out” equal areas in equal times.

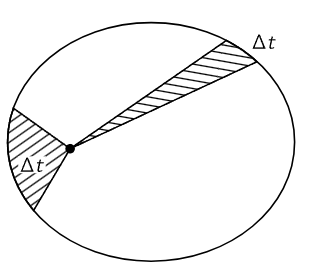
Fig. 7–2. Kepler’s law of areas.

Finally, a third law was discovered by Kepler much later; this law is of a different category from the other two, because it deals not with only a single planet, but relates one planet to another. This law says that when the orbital period and orbit size of any two planets are compared, the periods are proportional to the 3/2 power of the orbit size. In this statement the period is the time interval it takes a planet to go completely around its orbit, and the size is measured by the length of the greatest diameter of the elliptical orbit, technically known as the major axis. More simply, if the planets went in circles, as they nearly do, the time required to go around the circle would be proportional to the 3/2 power of the diameter (or radius). Thus Kepler’s three laws are:

1. Each planet moves around the sun in an ellipse, with the sun at one focus.
2. The radius vector from the sun to the planet sweeps out equal areas in equal intervals of time.
3. The squares of the periods of any two planets are proportional to the cubes of the semimajor axes of their respective orbits: T∝a^3/2.

__________________________________________________
margin

1- A radius vector is a line drawn from the sun to any point in a planet’s orbit.

مواضيع ذات صلة

Cosmic synchrotron radiation

Universal gravitation

The Relation of Physics to Astronomy

الكوارث الكونية والنجوم النيوترونية والثقوب السوداء

نشأة علم فلك الأشعة السينية

الجدات ورواد الفضاء

قانون الجذب العام (نيوتن وثمرة التفاح)

حساسات النانو في خدمة رحلات الفضاء الخارجي

الأجسام الصلبة والفضاء الخاوي

العوالم الأخرى: قد لا نكون بمفردنا في هذا الكون

كوكبة الحوت الجنوبي Piscis Australis

كوكبة الإكليل الجنوبي Corona Australis