Equilibrium Distribution of Electrons and Holes

Adding donor or acceptor impurity atoms to a semiconductor will change the distribution of electrons and holes in the material. Since the Fermi energy is related to the distribution function, the Fermi energy will change as dopant atoms are added. If the Fermi energy changes from near the midgap value, the density of electrons in the conduction band and the density of holes in the valence hand will change. These effects are shown in Figures 1.1 and 1.2. Figure 1.1 shows the case for E_F > E_Fi and Figure 1.2 shows the case for E_F < E_Fi. When E_F > E_Fi, the electron concentration is larger than the hole concentration, and when E_F < E_Fi, the hole concentration

Figure 1.1 Density of states functions. Fermi-Dirac probability function, and areas representing electron and hole concentrations for the case when E_F is above the intrinsic Fermi energy.

Figure 1.2 Density of states functions, Fermi-Dirac probability function, and areas representing electron and hole concentrations for the case when E_F is below the intrinsic Fermi energy.

is larger than the electron concentration. When the density of electrons 1s greater than the density of holes, the semiconductor is n type; donor impurity atom have been added. When the density of holes is greater than the density of electrons, the semiconductor is p type; acceptor impurity atoms have been added. The Fermi energy level in a semiconductor changes as the electron and hole concentrations change and, again, the Fermi energy changes as donor or acceptor impurities are added.

The expressions previously derived for the thermal-equilibrium concentration of electrons and holes, for n₀ and p₀ in terms of the Fermi energy. These equations are again given as

and

As we just discussed, the Fermi energy may vary through the handgap energy, which will then change the values of n₀ and p₀.

In this example, since n₀ > p₀, the semiconductor is n type. In an n-type semiconductor, electrons are referred to as the majority carrier and holes as the minority carrier. By comparing the relative values of n₀ and p₀ in the example, it is easy to see how this designation came about. Similarly, in a p-type semiconductor where p₀ > n₀, holes are the majority carrier and electrons are the minority carrier.

We may derive another form of the equations for the thermal-equilibrium concentrations of electrons and holes. We can write

(1a)

or

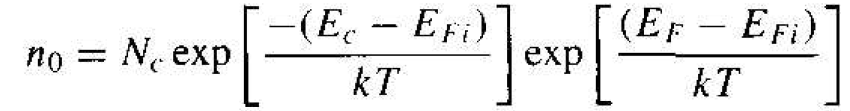(1b)

The intrinsic carrier concentration is given by

so that the thermal-equilibrium electron concentration can be written as

(2)

Similarly, if we add and subtract an intrinsic Fermi energy in the exponent, we will obtain

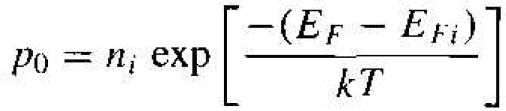(3)

As we will see, the Fermi level changes when donors and acceptors are added, but Equations (2) and (3) show that, as the Fermi level changes from the intrinsic Fermi level, n₀ and p₀ change from the n_i value. If E_F > E_Fi then we will have n₀ > n_i and p₀ < n_i. One characteristic of an n-type semiconductor is that E_F > E_Fi so that n₀ > p₀. Similarly, in a p type semiconductor, E_F < E_Fi SO that p₀ > n_i, an n₀ < n_i; thus p₀ > n₀.

We can see the functional dependence of n₀ and p₀ with E_F in Figures 1.1 and 1.2. As E_F moves above or below E_Fi , the overlapping probability function with the

density of states functions in the conduction band and valence band changes. As E_F moves above E_Fi, the probability function in the conduction band increases, while'

the probability, 1 - f_F(E), of an empty state (hole) in the valence band decreases. As E_F moves below E_Fi , the opposite occurs.