The k-Space Diagram

To begin to understand the nature of the solution, initially consider the special case for which V₀ = 0. In this case P' = 0. which corresponds to a free particle since there are no potential barriers. From Equation (24). we have that

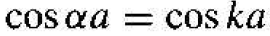(1)

or

(2)

Since the potentla1 is equal to zero, the total energy E is equal to the kinetic energy, so that, from Equation (5), Equation (26) may be written as

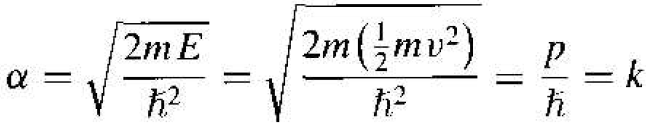(3)

where p is the particle momentum. The constant of the motion parameter k is related to the particle momentum for the free electron. The parameter k is also referred to as a wave number.

We can also relate the energy and momentum as

(4)

Figure 1.1 shows the parabolic relation of Equation (4) between the energy E and momentum p for the free particle. Since the momentum and wave number are linearly related, Figure 1.1 is also the E versus k curve for the free panicle.

We now want to consider the relation between E and k from Equation (24) for the particle in the single-crystal lattice. As the parameter P' increases, the particle becomes more tightly bound to the potential well or atom. We may define the left side of Equation (24) to be a function f (αa). so that

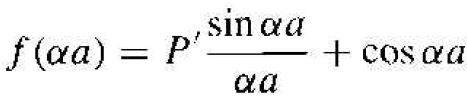(5)

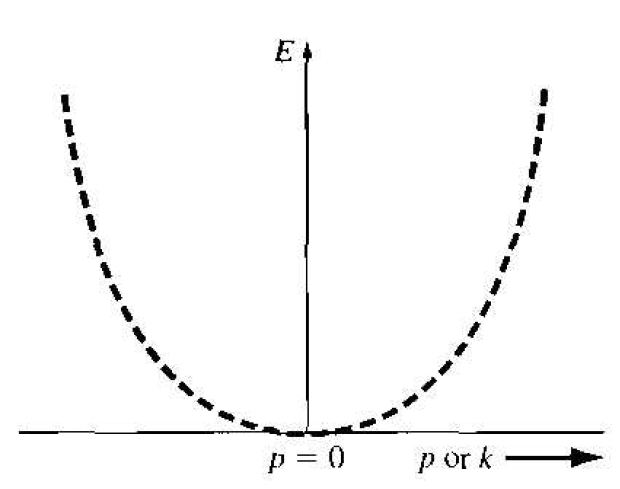
Figure 1.1 The parabolic E versus k curve for the free electron.

Figure 1.2  A plot of (a) the first term in Equation (5). (b) the second term in Equation (5). and (c) the entire f (αa) function. The shaded areas show the allowed values of (αa) corresponding to real values of k.

Figure 1.2a is a plot of the first term of Equation (5) versus au. Figure 1.2b shows a plot of the cos a u term and Figure 1.2c is the sum of the two terms, or f (αa).

Now from Equation (24). we also have that

(6)

For Equation (6) to be valid, the allowed values of the f (αa) function must be

bounded between + 1 and -1. Figure 1.2c shows the allowed values of f (αa) and the allowed values of αa in the shaded areas. Also shown on the figure are the values of ka from the right side of Equation (6) which correspond to the allowed values of f (αa).

The parameter α is related to the total energy E of the particle, which is α² = 2m E/h². A plot of the energy E of the particle as a function of the wave number k can be generated from Figure 1.2c. Figure 1.3 shows this plot and shows the concept of allowed energy bands for the particle propagating in the

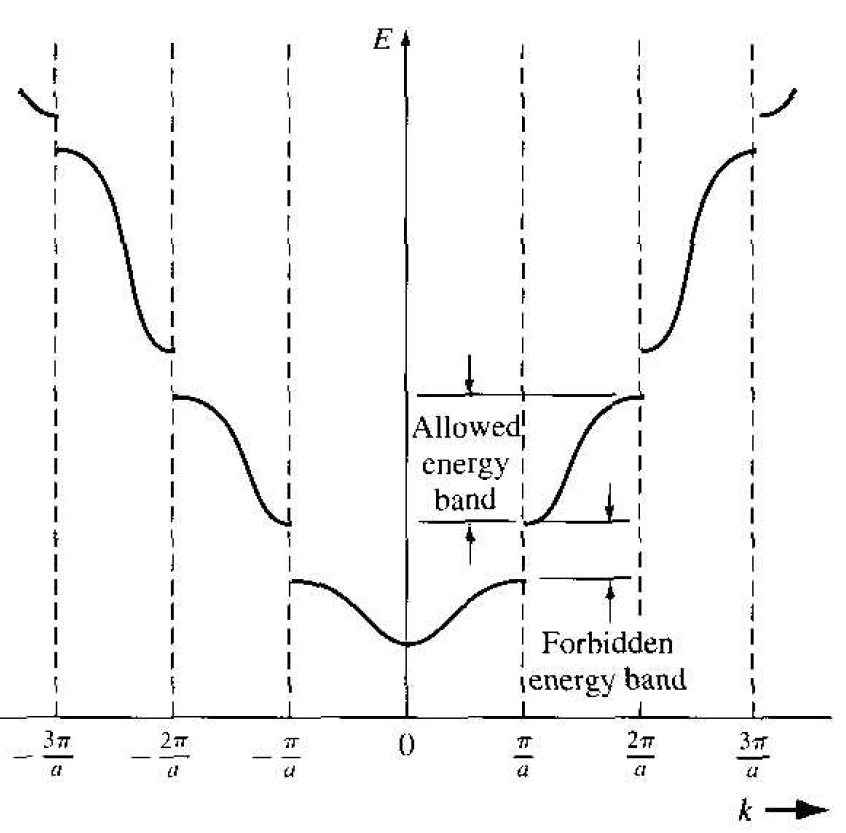
Figure 1.3  The E versus k diagram generated from Figure 1.2. The allowed energy bands and forbidden energy bandgaps are indicated.

crystal lattice. Since the energy E has discontinuities, we also have the concept of forbidden energies for the particles in the crystal.

Consider again the right side of Equation (24), which is the function cos ka. The cosine function is periodic so that

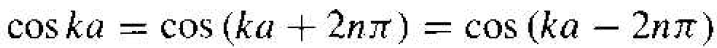(7)

where n is a positive integer. We may consider Figure 1.3 and displace portions of the curve by 2π. Mathematically, Equation (24) is still satisfied. Figure 1.4 shows how various segments of the curve can be displaced by the 2π factor. Figure 1.5 shows the case in which the entire E versus k plot is contained within -π/a < k < π/a. This plot is referred to as a reduced k-space diagram, or a reduced-zero representation.

We noted in Equation (3) that for a free electron, the particle momentum and the wave number k are related by p = hk. Given the similarity between the free

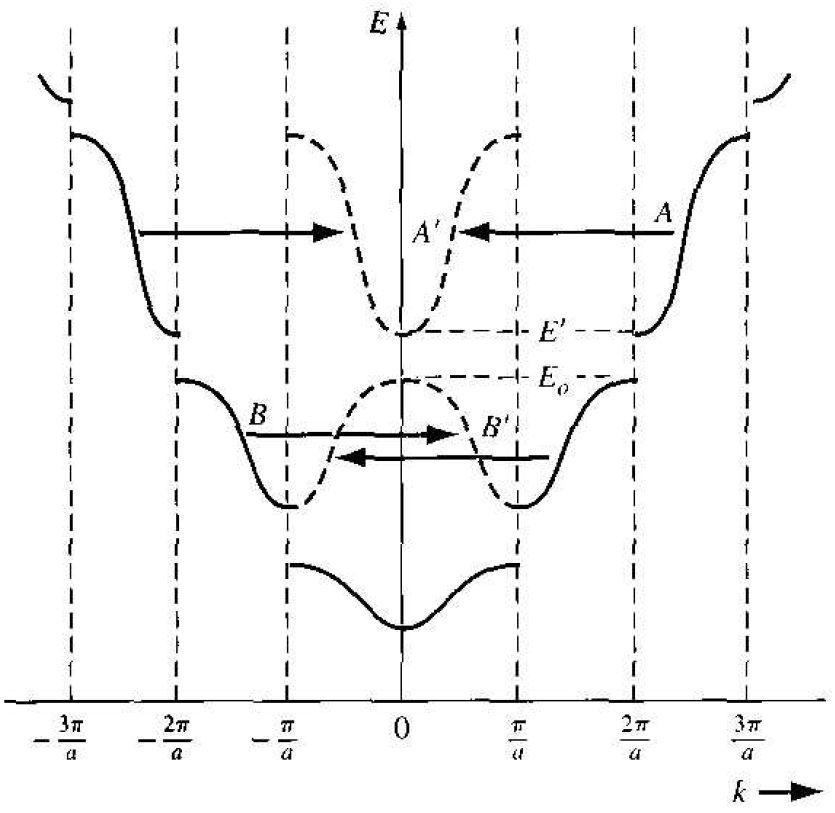
Figure 1.4 The E versus k diagram showing 2π displacements of several sections of allowed energy bands.

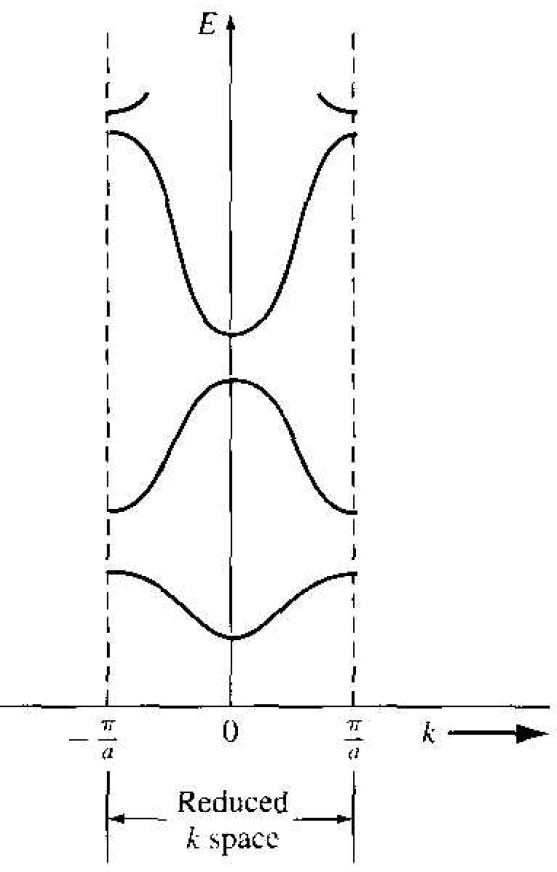
Figure 1.5  The E versus k diagram in the reduced-zone representation.

electron solution and the results of the single crystal shown in Figure 1.3, the parameter hk in a single crystal is referred to as the crystal momentum. This parameter is not the actual momentum of the electron in the crystal, but is a constant of the motion that includes the crystal interaction.

We have been considering the Kronig-Penney model, which is a one dimensional periodic potential function used to model a single-crystal lattice. The principle result of this analysis, sofa,: is that electrons in the crystal occupy certain allowed energy bands and are excluded from the forbidden energy bands. For real three-dimensional single-crystal materials, a similar energy-band theory exists. We will obtain additional electron properties from the Kronig-Penney model in the next sections.