If you were to simply solve from left to right, the answer would be incorrect. Let's do that now. 14 + 6 = 20. Divide that by 5 to get 4. Multiply 4 times 11 to get 44. Subtract 7 to get 37, and divide by 3 to get 12.333. (THIS IS WRONG!)

The order of operations will allow you to solve this problem the right way. The order is this: Parenthesis, Exponents, Multiplication and Division, Addition and Subtraction. Always perform the operations inside a parenthesis first, then do exponents. After that, do all the multiplication and division from left to right, and lastly do all the addition and subtraction from left to right.

A popular way of remembering the order is by putting together the first letter of each word: PEMDAS. You can also create a little phrase to go along with this, like "Please Excuse My Dear Aunt Sally." Whatever you choose, make sure that you know all six steps of the order of operations very well.

Let's try solving that equation again, this time using PEMDAS.

Step 1) Parenthesis. There aren't any. Move on.
Step 2) Exponents. None. Keep going.
Step 3) Multiplication and Division. Go from left to right, so divide 6 by 5 to get 1.2, and multiply that by 11 to get 13.2. Don't forget to divide 7 by 3 to get 7/3 (about 2.33).
Step 4) Addition and Subtraction. From left to right, 14 + 13.2 = 27.2, subtract 7/3 and get your answer: about 24.867.

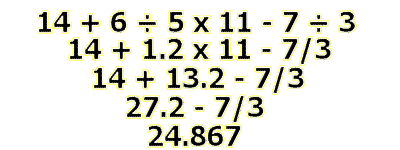
The whole idea is just to follow the rule: PEMDAS. Now we can try to solve one with parenthesis and exponents on the next page.

What if you are given an equation like the one below? Just simplify it in small steps, using the order of operations at all times.

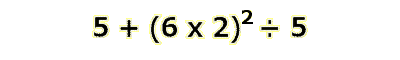
Remember, the first step is Parenthesis. Look inside the parenthesis, where we have 6 x 2. That comes out to 12. We can then square 12 to get 144, making this equation easy to finsh.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم صناعة الشبابيك يشرع بإدامة شباكين قديمين لمرقد الإمامين العسكريين (عليهما السلام)

فرقة العباس (عليه السلام) تختتم خدماتها المقدمة للزائرين في سامراء

موكب العتبتين المقدستين يحيي ذكرى استشهاد الإمام الهادي (عليه السلام) في سامراء

العتبة العسكرية المقدسة تكرّم وفد العتبة العباسية المقدسة لمشاركته في تقديم الخدمات للزائرين

المزيد

الآخبار الصحية

كنز غذائي على طبقك.. ماذا تفعل السبانخ بجسمك؟

ما لا يتوقعه أحد.. "سر غذائي" في الجبن الدسم

لتحسين الهضم والنوم.. هذا أفضل وقت لتناول العشاء

10 طرق بسيطة وغير مألوفة لحرق المزيد من السعرات يوميا

المزيد

الآخبار التكنلوجية

سابقة بعالم الطيران.. طائرة تقرر الهبوط بنفسها بعد ظرف طارئ

"الإنفلونزا الخارقة" تكتسح دول العالم.. وتثير قلقا كبيرا

مرحلة ما قبل الأعراض.. دواء جديد يستهدف "شرارة" الزهايمر

إزالة ثاني أكسيد الكربون من الغلاف الجوي.. ما دور المحيطات والبحار؟

المزيد

مواضيع ذات صلة

Zero Set

Xi-Function

Weierstrass Product Theorem

Tangent

Tanc Function

Simple Root

Separation Theorem

Rouché,s Theorem

Root Linear Coefficient Theorem

Root

Multiplicity

Multiple Root