


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 14-9-2016
Date: 23-2-2017
Date: 19-8-2016
|
The Kepert model
For many years after the classic work of Werner which laid the foundations for the correct formulation of d-block metal complexes , it was assumed that a metal in a given oxidation state would have a fixed coordination number and geometry. In the light of the success (albeit not universal success) of VSEPR theory in predicting the shapes of molecular species of the p-block elements, we might reasonably expect the structures of the complex ions [V(H2O(6]3+ (d2), Mn)H2O(6]3+ (d4), [Co(H2O)6]3+ (d6), [Ni(H2O)6]2+ (d8) and [Zn(H2O)6]2+ (d10) to vary as the electronic configuration of the metal ion changes. However, each of these species has an octahedral arrangement of ligands (1.1). Thus, it is clear that VSEPR theory is not applicable to d-block metal complexes.

(1.1)
We turn instead to the Kepert model, in which the metal lies at the centre of a sphere and the ligands are free to move over the surface of the sphere. The ligands are considered to repel one another in a similar manner to the point charges in the VSEPR model; however, unlike the VSEPR model, that of Kepert ignores non-bonding electrons. Thus, the coordination geometry of a d-block species is considered by Kepert to be independent of the ground state electronic configuration of the metal centre, and so ions of type [MLn]m+ and [MLn]m- have the same coordination geometry.
The Kepert model rationalizes the shapes of d-block metal complexes [MLn], [MLn]m+ or [MLn]m- by considering the repulsions between the groups L. Lone pairs of electrons are ignored. For coordination numbers between 2 and 6, the following arrangements of donor atoms are predicted:
2 linear
3 trigonal planar
4 tetrahedral
5 trigonal bipyramidal or square-based pyramidal
6 octahedral
Table 1.4 lists coordination environments associated with coordination numbers between 2 and 9; not all are predictable using the Kepert model. For example, after considering the repulsions between the cyano ligands in [Cu(CN(3]2- , the coordination sphere would be predicted to be trigonal planar (1.2). Indeed, this is what is found experimentally. The other option in Table 1.4 is trigonal pyramidal, but this does not minimize interligand repulsions. One of the most important classes of structure for which the Kepert model does not predict the correct answer is that of the square planar complex, and here electronic effects are usually the controlling factor.. Another factor that may lead to a breakdown of the Kepert model is the inherent constraint of a ligand.
For example:
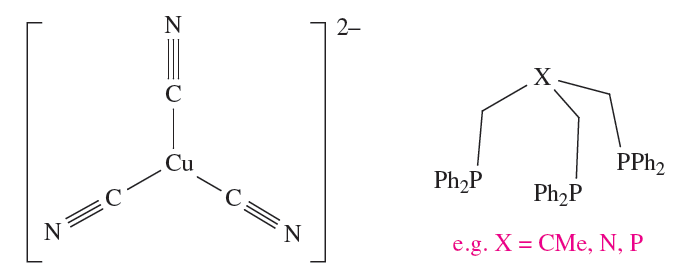
(1.2) (1.3)
A tripodal ligand (e.g. 1.3) is one containing three arms, each with a donor atom, which radiate from a central atom or group; this central point may itself be a donor atom. In the remaining part of this section, we give a systematic outline of the occurrence of different coordination numbers and geometries in solid state d-block metal complexes. A general word of caution: molecular formulae can be misleading in terms of coordination number. For example in CdI2, each Cd centre is octahedrally sited, and molecular halides or pseudo-halides (e.g. [CN]-) may contain M_X_M bridges and exist as oligomers, e.g. α-PdCl2 is polymeric (1.4).
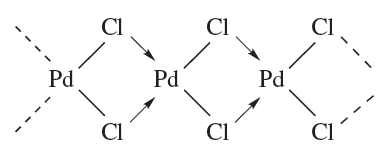
(1.4)
A further ambiguity arises when the bonding mode of a ligand can be described in more than one way. This often happens in organometallic chemistry, for example with cyclopentadienyl ligands, there is still the question of whether to consider, for example, an [η5-C5H5]- ligand as occupying one or five sites in the coordination sphere of a metal atom: thus, the coordination number of the Ti(IV) centre in [(η5-C5H5)2TiCl2] may be represented as either 1.5a or 1.5b.
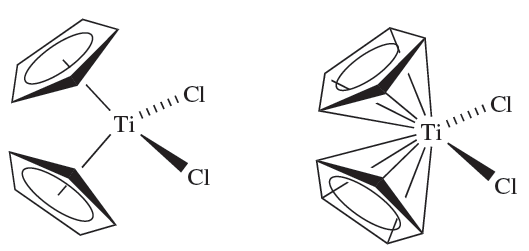
(1.5a) (1.5b)


|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|