
Complexes with no metal–ligand π-bonding
 المؤلف:
CATHERINE E. HOUSECROFT AND ALAN G. SHARPE
المؤلف:
CATHERINE E. HOUSECROFT AND ALAN G. SHARPE
 المصدر:
INORGANIC CHEMISTRY
المصدر:
INORGANIC CHEMISTRY
 الجزء والصفحة:
2th ed p 564
الجزء والصفحة:
2th ed p 564
 14-9-2016
14-9-2016
 1321
1321
Complexes with no metal–ligand π-bonding
We illustrate the application of MO theory to d-block metal complexes first by considering an octahedral complex such as [Co)NH3(6]3+ in which metal–ligand π-bonding is dominant. In the construction of an M energy level diagram for such a complex, many approximations are made and the result is only qualitatively accurate. Even so, the results are useful to an understanding of metal–ligand bonding. For a first row metal, the valence shell atomic orbitals are 3d, 4s and 4p. Under Oh symmetry, the s orbital has a1g symmetry, the p orbitals are degenerate with t1u symmetry, and the d orbitals split into two sets with eg (dz2 and dx2-y2 orbitals) and t2g (dxy, dyz and dxz orbitals) symmetries, respectively (Figure 1.1). Each ligand, L, provides one orbital and derivation of the ligand group orbitals for the Oh L6 fragment is analogous to those for the F6 fragment in SF6. These LGOs have a1g, t1u and eg symmetries (Figure 1.1).
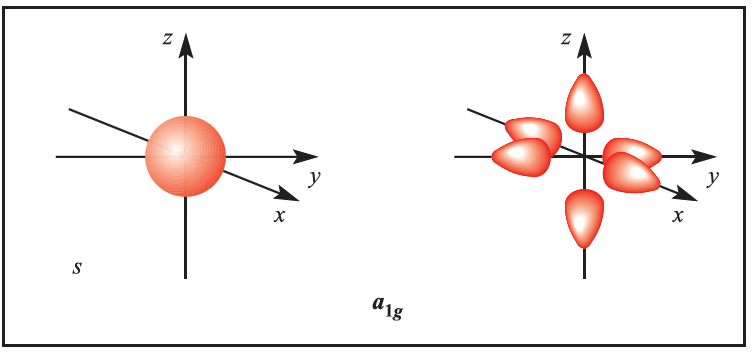
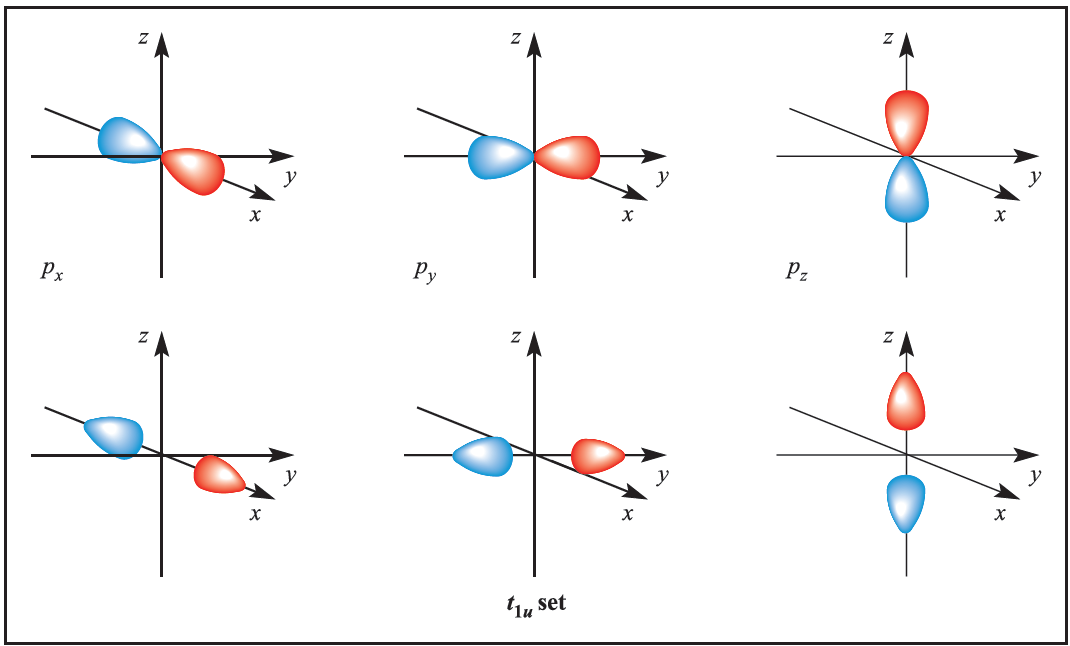

Fig. 1.1 Metal atomic orbitals s, px, py, pz, dx2 _y2 , dz2 matched by symmetry with ligand group orbitals for an octahedral(Oh)complex with only π-bonding.
Symmetry matching between metal orbitals and LGOs allows the construction of the MO diagram shown in Figure 1.2. Combinations of the metal and ligand orbitals generate six bonding and six antibonding molecular orbitals. The metal dxy, dyz and dxz atomic orbitals have t2g symmetry and are non-bonding (Figure 1.2).
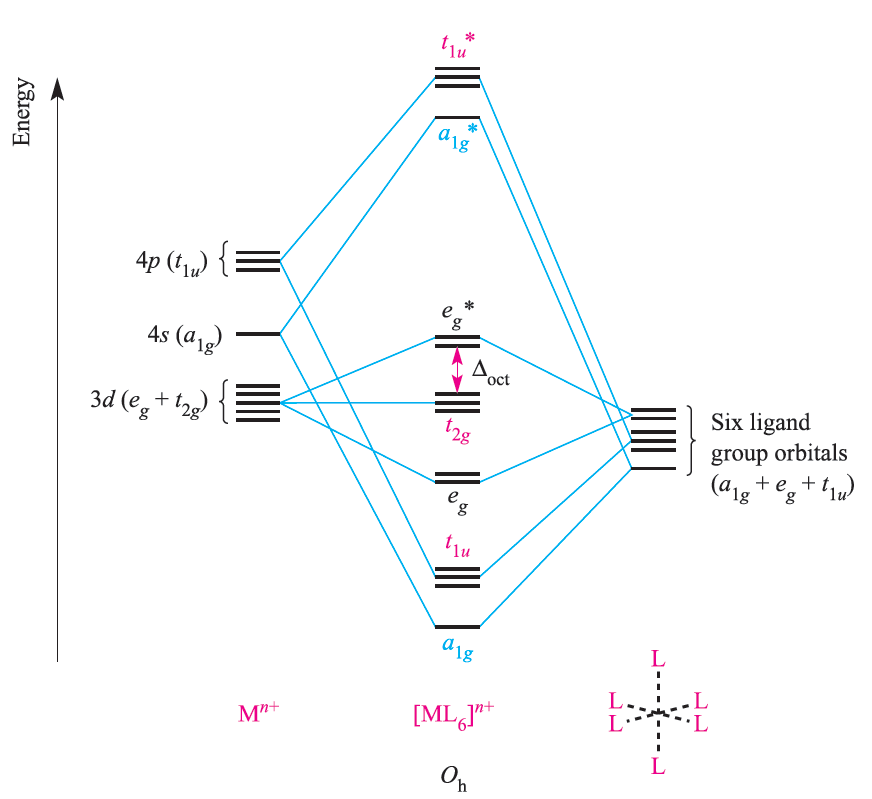
Fig. 1.2 An approximate MO diagram for the formation of [ML6]n+ (where M is a first row metal) using the ligand group orbital approach; the orbitals are shown pictorially in Figure 1.1. The bonding only involves M_L π-interactions.
The overlap between the ligand and metal s and p orbitals is greater than that involving the metal d orbitals, and so the a1g and t1u MOs are stabilized to a greater extent than the eg MOs. In an octahedral complex with no π-bonding, the energy difference between the t2g and eg* levels corresponds to Δoct in crystal field theory (Figure 1.2). Having constructed the MO diagram in Figure 1.2, we are able to describe the bonding in a range of octahedral σ- bonded complexes. For example:
- in low-spin [Co(NH3)6]3+, 18 electrons (six from Co3+ and two from each ligand) occupy the a1g, t1u, eg and t2g MOs;
- in high-spin [CoF6]3-, 18 electrons are available, 12 occupy the a1g, t1u and eg MOs, four the t2g level, and two the eg* level.
Whether a complex is high- or low-spin depends upon the energy separation of the t2g and eg* levels. Notionally, in a σ-bonded octahedral complex, the 12 electrons supplied by the ligands are considered to occupy the a1g, t1u and eg orbitals. Occupancy of the t2g and eg* levels corresponds to the number of valence electrons of the metal ion, just as in crystal field theory. The molecular orbital model of bonding in octahedral complexes gives much the same results as crystal field theory. It is when we move to complexes with M_L π-bonding that distinctions between the models emerge.
 الاكثر قراءة في كيمياء العناصر الانتقالية ومركباتها المعقدة
الاكثر قراءة في كيمياء العناصر الانتقالية ومركباتها المعقدة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


