As an example, consider a coordinate plane with an x-axis and a y-axis; then we can identify any point in the plane by its coordinates 〈x, y〉. If you wanted to find〈〉

the point 〈a,b〉, you would move on the x-axis a units to the right or to the left from the origin (depending on the sign of a), and then you would move b units up or down. If a and b are different, then 〈a,b〉and 〈a,b〉denote different points. So, in this example the order in which the elements appear is relevant. This leads to the following

Definition 1.1. Let A be a set;

1. A is called a singleton if A = {x} for some x, i.e. if A has exactly one element.

2. A is called an unordered pair, if A = {x,y} for some x,y, if A has exactly two elements.

3. A is called an ordered pair if A = {{x}, {x,y}} for some x,y.

We shall usually abbreviate the right hand expression by

                                            〈 x,y〉 = {{x}, {x, y}}.

The decisive property of ordered pairs is that two ordered pairs are equal if the respective components are the same. The following Theorem assures us, that the ordered pair as we have defined it has this property:

Theorem 1.1. Let 〈a,b〉and (c,d) be ordered pairs. Thenha, bi = 〈 c,d〉 if and only if a = c and b = d.

Remark. The expression “if and only if” means that

1. If 〈a,b〉= 〈 c,d〉, then a = c and b = d.

2. If a = c and b = d, then 〈a,b〉= 〈c, d〉. (This is called "the converse" of 1.)

So, we have to prove two directions, namely 1. and 2. Usually, “if and only if” is abbreviated as simply “iff”.

Proof. “⇒”: Suppose 〈a,b〉= 〈c, d〉; then, by definition,

〈a,b〉=  {{a}, {a,b}},

〈c, d〉= {{c}, {c,d}},

and since they are equal by our hypothesis, we have

{{a}, {a,b}} = {{c}, {c,d}}.

We consider two cases:

1. a = b: Then,

〈a,b〉= {{a}, {a,b}} = {{a}} = {{c}, {c, d}},

hence, {a} = {c} which implies a = c. Furthermore, {a} = {c,d} = {a,d} which implies d = a = b. Thus, for this case we have shown that a = c and b = d.

2. a ≠b: Then, {a} ≠{a,b}. By our hypothesis we must have {a} = {c}, since both sets have only one element; this implies a = c.

Furthermore, {a, b} = {c,d}, since {a,b} has two elements. We have just shown that a = c, thus, {a,b} = {c, b} = {c,d}. This implies b = d, and this is what we wanted to show.

“⇐”: For the converse, let a = c and b = d; then, {a} = {c}, and {a,b} = {c,d},

hence,

〈a,b〉= {{a}, {a,b}} = {{c}, {c,d}} = 〈c, d〉

which is what we wanted to show.

You need only remember the property of ordered pairs given in the preceding Theorem;

it is not necessary to remember the set theoretic definition.

Definition 1.2. The Cartesian (or cross-) product A × B of two sets is defined

as

                 A × B = {〈a,b〉: a ∈ A, b ∈ B}

So, the operation × pairs the elements of A with the elements of B in such a way that the elements of A appear as first components, and the elements of B appear as second components. It is also possible to define Cartesian products for more than two factors, but we shall not do this at this stage.

Example.1. 1. Let A = {1, 2, 3} and B = {a,b}; then

2. Let A = R and B = R; then A × B = R × R is the set of all points in the Cartesian coordinate plane.

3. Let 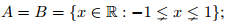  then A × B is the set of all points in

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

Subset

Set Class

Set

Second Category

Proper Subset

Power Set

Matroid

Inductive Set

Independent Vertex Set

Independent Set

Graphoid

G_delta Set