
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Beyond the point mass lens approximation
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 271
6-2-2017
2239
Beyond the point mass lens approximation
Up to now, we have considered only the simple case of lensing by a point mass. There are two reasons to explore more complicated models. The first is that it
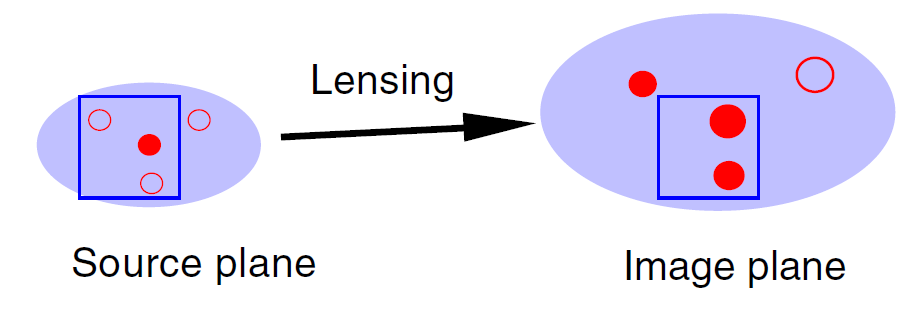
Figure 1.1. The magnification bias in star counts due to gravitational lensing. Stars (circles) are counted in a field of a fixed angular area (square) with a telescope of a given photometric detection threshold. The field in the unlensed sky (source plane, left), contains one bright star that can be observed (filled circle) and two stars that are too faint to be observed (open circles). Gravitational lensing stretches angular areas and magnifies fluxes by the same factor. The field in the lensed sky (image plane, right), now contains only two stars, but because they are magnified, both can be observed. This is an example of positive magnification bias, where gravitational lensing increases the apparent stellar surface density even as it decreases the total surface density. Negative magnification bias occurs when there are not enough faint stars in the lensed population to compensate for the decrease in the total surface density.
would be useful if gravitational lensing could be used to dispel any remaining doubts that the dark compact mass in the Galactic Center is indeed a MBH, and not some other extended distribution of matter, such as a compact cluster of stellar remnants (Maoz 1998) or a concentration of exotic particles (Tsiklauri and Viollier 1998). Unfortunately, it can be shown that the behavior of high magnification light curves near peak magnification is universal and independent of the details of the lens. For spherically symmetric mass distributions this implies that the light curves differ only in the low magnification tails, which are much harder to observe. The second reason is that the MBH is surrounded by a massive stellar cluster. Because the stellar mass is not smoothly distributed but is composed of discrete point masses, its effect on the lensing properties of the MBH is much larger than one may naively estimate by adding the stellar mass to that of the MBH. We conclude the discussion of gravitational lensing in the Galactic Center by describing briefly the effect of enhanced lensing by stars near the MBH (Alexander and Loeb 2001, Chaname et al 2001).
The effect of stars on lensing by the MBH is similar to that of planets on microlensing by a star, an issue that was studied extensively for the purpose of detecting planets by microlensing (e.g. Gould and Loeb 1992). The lensing cross section of an isolated star is θ2E(M*)/θ2E(M●) = M*/M● < 10−6 smaller than that of the MBH. However, when the star lies near θ(M●), the shear of the MBH distorts its lensing cross section, which develops
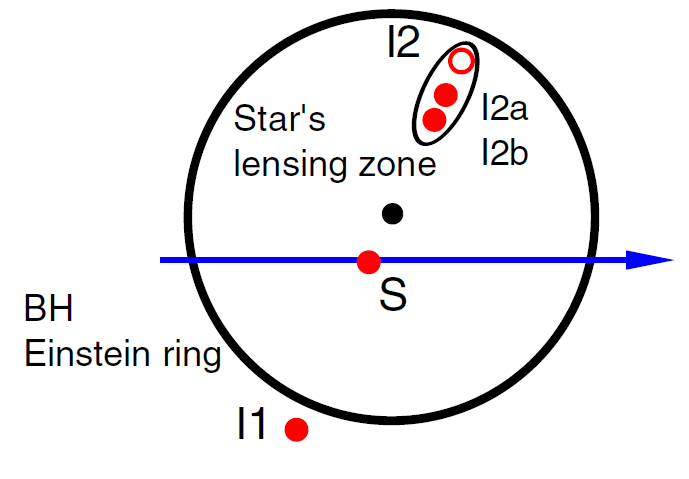
Figure 1.2. A schematic representation of lensing enhancement by a star near the MBH (Alexander and Loeb 2001, Chaname et al 2001). A light source S passes behind the MBH (filled circle in the middle) and, in the absence of any other lensing mass, appears as two images: I1 outside the Einstein ring and I2 inside the Einstein ring. When one of the stars near the MBH happens to lie (in projection) close to I2, it will split I2 into two or four sub images (two shown here), I2a and I2b. The star's Einstein ring is sheared by the potential of the MBH to an elongated shape of complex topology (represented here for simplicity as an ellipse), which increases in size the nearer I2 and the star are to the Einstein radius of the MBH. This effect increases the cross section for high-magnification events above that of an isolated MBH, and changes the character of the light curves.
a complex topology, becomes radially elongated and is increased by up to an order of magnitude (figure 1.2). As the stars orbit the MBH, their elongated cross sections scan the lens plane. If these happen to intersect one of the images of a background source that is lensed by the MBH, the image will be split into two or four sub images whose angular separation will be of order θE(M*), and so the sub-images will not be individually resolved. However, their combined flux will be significantly magnified. This will increase the probability of high magnification events over what is expected for lensing by the MBH alone. The light curves of such events will no longer be symmetric as they are for a point mass, but will exhibit a complex structure (e.g. Wambsganss 1997), and their typical variability timescales will rise sharply for images that lie near θE(M● because of the increased stellar cross section for lensing. Enhanced lensing by stars in the Galactic Center is estimated to increase the probability of A > 5 lensing events by ∼2 and of A > 50 events by ∼3.
 الاكثر قراءة في مواضيع عامة في علم الفلك
الاكثر قراءة في مواضيع عامة في علم الفلك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















