


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-12-2015
Date: 6-2-2017
Date: 23-12-2015
|
Motion of ultrarelativistic particles
1.1 Equations of motion
When the energy E is much larger than m, a particle is called ultrarelativistic. In this limit Ẽ → ∞ and ˜L → ∞while the ratio ˜L /Ẽ remains finite and is equal to ˜b := b/rS, where b is the impact parameter of the particle at infinity. The equations of motion of the ultrarelativistic particle (or a light ray) take the form (˜t = t/rS):
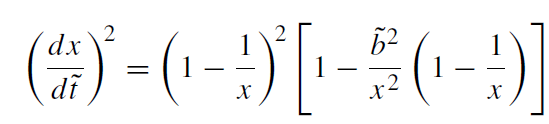 (1.1)
(1.1)
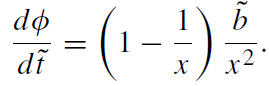 (1.2)
(1.2)
The sign of b depends on the sense of motion; we assume that b is positive. The radial turning point on the trajectory is defined by the equation
 (1.3)
(1.3)
The impact parameter b as a function of the position of a radial turning point is shown in figure 1.1.
1.2 Types of trajectory
In figure 1.1, the motion of an ultrarelativistic particle with a given b is represented by a horizontal line b = constant. A particle approaches the black hole,

Figure 1.1. Impact parameter b as a function of the position of extrema in x = r/rS on the trajectory of an ultrarelativistic particle.
passes by it at the minimal distance corresponding to the point of intersection of b = constant with the right-hand branch of the b(r ) curve, and again recedes to infinity. If the intersection occurs close to the minimum bmin = 3√3 × rS/2, the particle may experience a number of turns before it flies away to infinity. The exact minimum of the curve b(r) corresponds to the (unstable) motion on a circle of radius r = 1.5rS at the velocity v = c. Note that the left-hand branch of b(r) in figure 1.1 corresponds to the maximum distance between the ultrarelativistic particle and the black hole; the particle first recedes to r < 1.5rS but then again falls into the black hole. Obviously, for such a motion the parameter b does not have the literal meaning of the impact parameter at infinity since the particle never recedes to infinity. For a given coordinate r , this parameter can be found as a function of the angle ψ between the trajectory of the particle and the direction to the center of the black hole:
 (1.4)
(1.4)
If an ultrarelativistic particle approaches the black hole on the way from infinity and the parameter b is less than the critical value bmin = 3√3rS/2, the particle falls into the black hole.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|