The problem of designing a circuit that has given properties is exactly that of finding the proposition which has a given truth table. The first step is to construct the table which gives the desired state (represented as 0 or 1) of the circuit for each possible assignment of states for the separate switches. The Boolean function corresponding to the table is then written and, if possible, simplified. From the simplified expression a circuit is drawn. Further simplifications may be possible by using non-series-parallel circuits such as the bridge in Section (Non-series-parallel circuits), but here the problem depends more upon the ingenuity of the designer than upon Boolean algebra.

EXAMPLE 1. It is desired to design a circuit connecting two switches and a light bulb in such a way that either switch may be used to control the light independently of the state of the other.

Solution. If we designate the two switches by x and y, Table 1-1 corresponds to a suitable function. The reasoning by which the table is constructed goes as follows. The functional value in row 1 is arbitrary if we do not care whether the light is on or off for any given position of the switches. If we assign the value 1, then either row 2 or row 3 represents a change of state of a single switch, and this is required to change the state of the light. Hence, 0 is the proper functional value for rows 2 and 3. Finally, row 4 represents a change of state of a single switch from the state of either row 2 or row 3. Hence, the function must assume the value 1 in row 4. The function is now written as f = zy + x'y'. It is interesting to note that this problem is logically equivalent to the "snake-in-the-box" problem in Section 3-3. The circuit may be drawn as in Fig. 1-1. However, the diagram of Fig. 4-31 is perhaps more suggestive of the actual wiring that is required. The switch pairs (x, z') and (y, y') each consists of a single-pole double-throw switch. The symbol 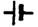is the usual one indicating a current source.

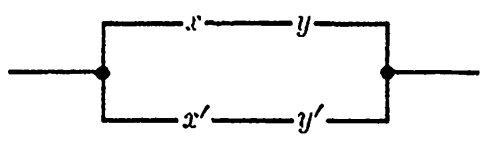
FIG. 1-1. Control circuit for a 2-way light switch.

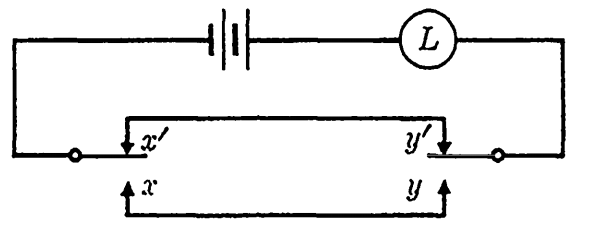
FIG. 1-2. Alternative diagram for the circuit of Fig. 1-1.

It often happens that in the design of a switching circuit, it is known that certain combinations of states of switches will never occur. When this happens, the function chosen for the design may take on either of the values 0 or 1 for such combinations without affecting the results.  We will represent such combinations by placing the symbol (?) in the function column of the table of closure properties. A suitable choice of values

TABLE 1-1                                                                  TABLE 1-2

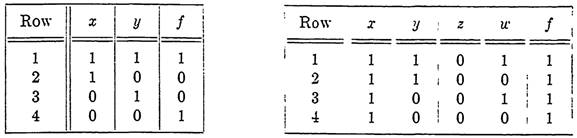
corresponding to the rows marked with (?) may greatly simplify the resulting circuit. A formal set of rules could be stated which would completely solve this problem, but we will give just two rules which are often of considerable help.

RULE 1. If it is possible to assign all 0's or all 1's and thereby leave a small number of rows having value 1 (or 0) while all others have the complementary value, then a correspondingly simple disjunctive normal form (or conjunctive normal form) will give the function.

RULE 2. It may be possible to assign 0's and 1's in a fashion to makethe function independent of one or more letters, thereby simplifying the resulting circuit.

The application of Rule 1 is obvious. In applying Rule 2, we will think entirely in terms of writing the function in disjunctive normal form.  If this form contains two terms alike except for one variable, then that variable may be eliminated. For example xyz' + xyz = xy(z + z') = xy.  This corresponds to saying that if two rows of the table for which the function takes the value 1 are alike except for the state of a single switch,  then the two rows can be represented by a single term independent of the variable representing that switch. Similarly, if four rows for which the function takes the value 1 are alike except for the states of two switches,  then the four rows can be represented by a single term independent of the two variables corresponding to these switches. The reason for this is that the columns corresponding to like states will be represented by common factors in the disjunctive normal form, and the remaining variables will appear only in a factor which is the complete disjunctive normal form in these variables and hence may be deleted. Consider the four rows of Table 1-2, for instance. Representing the rows directly, we obtain

            xyz'w + xyz'w' + xy'z'w + xy'z'w' = xz'(yw + yw' + y'w + y'w') = xz'.

This simplification can be performed by inspection, thus avoiding the necessity of writing the longer expression. The method can be extended to the case where 2" rows are alike except for the states of n switches,  but it becomes increasingly more difficult to isolate such possibilities by the inspection of a table. This method, of course, applies also in cases where no ? appears in any row whenever like rows are present.  A final help in constructing a function for a given table comes from noting that if any letter, say .r, has the value 1 in every row for which the function is 1, then r is a factor of the function. Similarly, if every row shows the value 0 for .r, then x' is a factor of the function.

EXAMPLE 2. Design a circuit having the properties given in Table 1-3.

Table 1-3

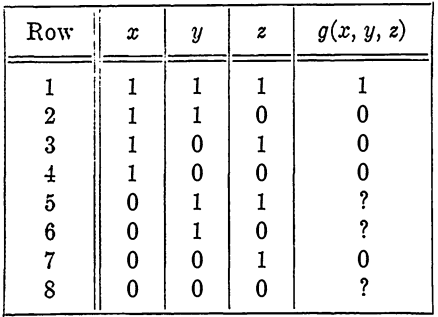
Solution 1. Using Rule 1 and noting that only a single 1 appears in the function column, if we assign 0 to each ? the function f = xyz will result. The circuit is a series connection of switches x, y, and z.

Solution 2. If we use Rule 2 and note that if we assign 1 to row 5 and 0 to each of rows 6 and 8, the function becomes independent of x and may be written as f = yz. The circuit is now a series connection of y and z only, which is simpler than the circuit of Solution 1. Of course, the two circuits are not equivalent, but they differ only in the cases that do not arise, and hence either will serve.

It is unnecessary to list an entire table of closure properties. It is sufficient merely to list those rows for which the function is 1, assuming that all unlisted rows correspond to combinations for which the function is to be 0. This practice will be adopted in the future wherever it is convenient.