When two or more relays are to be controlled from common inputs, n-terminal circuits arise naturally from the attempt to be economical in the use of contacts. Such circuits are of the type discussed in (Design of n-terminal circuits). In this section, wewill use a number of examples to illustrate methods which may be used in designing control circuits and to show difficulties which may arise.

EXAMPLE 1. Two relays X and Y are to be controlled from contacts on relays A, B, C, and D representing input conditions. We are to design a control circuit such that X will be operated when A is operated and B is released, and Y will be operated if both A and C are operated or if D is released.

FIG. 1-1. Separate control circuits for two relays.

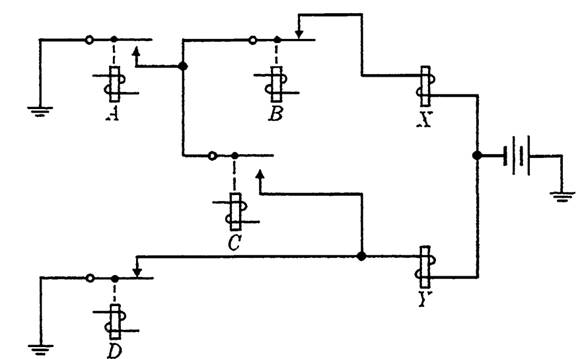
FIG. 1-2. Combined control circuits involving a sneak path.

Solution. Denote the control function for X by x(a, b), and for Y by y(a, c, d).  From the given conditions, x(a, b) = ab' and y(a, c, d) = ac + d'. The separate circuits are shown in Fig. 1-1. These circuits would require two make contacts on relay A if drawn separately, but may be combined as in Fig. 1-2 with only a single make. This small saving in contacts would become significant if, instead of a single contact a, the common part of the circuits were a more complicated circuit. The difficulty in this circuit is that relay X will now operate if C is operated while B and D are released, which was not intended. Such a path is termed a sneak path. We can eliminate this sneak path with the use of a transfer contact on D, as illustrated in Fig. 1-3. Since the path through A and C is important only when D is operated, the circuit is equivalent. Or, we may show this algebraically since y(a, c, d) = ac + d' = acd + d', where the second expression represents the new path. Even though this last circuit uses an extra contact on D, a reduction in total number of contacts would result if A represented a circuit containing two or more contacts instead of a single contact. Another possible way to eliminate the sneak path, where direct current is used in the circuit, would be to place a rectifying diode in the circuit of Fig. 1-2 between C and A. A rectifying diode is a device having a very high resistance to current in one direction, and practically no resistance to current in the other direction. Of course, such an element would add to the cost of the circuit.

FIG. 1-3. Combined circuit with sneak path eliminated by a transfer contact.

This example illustrated a situation in which two control paths can be combined without interfering with each other. (This may happen in any of several sets of circumstances, some of which are listed below.) In this case, the combination is possible because the two leads to ground for relay Y consist of disjunctive paths. We will say that two paths are disjunctive if each path passes through a contact on a common relay, one using a make and the second a break contact. In terms of the functions representing the circuits, this condition is equivalent to the condition that two functions contain respectively the factors a and a' for some relay A. In such cases a transfer contact will usually be used because it requires one less spring and ensures that the two paths cannot be simultaneously closed. With separate make and break contacts, it is possible that the circuits would be simultaneously closed for a short time due to contact stagger, allowing the make to close before the break opens.

Three simple cases in which two control paths may be combined without sneak paths are listed below. Let the corresponding control functions be f and g, the functions representing the control paths for relays X and Y respectively.

I. f and g contain common factors.

EXAMPLE 2. Suppose that f = (ab + a'b')c and that g = (ab + a'b')d. The combined circuit is given in Fig. 1-4.

FIG. 1-4. Combined control paths (ab +a'b')c and (ab +a'b')d.

II. Summands of f and g contain common factors, and these summands are disjunctive.

EXAMPLE 3. Suppose that f = (a + b)c + d and that g = (a +b)c' + e.

Since (a + b)c and (a + b)c' are disjunctive, the circuits may be combined as in Fig. 1-5.

FIG. 1-5. Combined control paths (a + b)c + d and (a + b) c' + e.

III. Summands of f and g contain common factors, and this summand off (or of g) is disjunctive with the remaining summand off (or of g).

EXAMPLE 4. We need only refer to Example 1, where x(a, b) and y(a, c, d)  illustrate such control functions, and the circuits of Fig. 1-3 show the method of construction, using a transfer contact.

In summary, we can say that two or more 2-terminal control circuits may often be combined in part with a net saving of contacts. Possible combinations can be spotted by examining the Boolean functions representing the circuits. In combining control circuits, sneak paths should be avoided unless it is known that the combination leading to closure of the sneak path will not arise. Transfer contacts are extremely useful in keeping parts of an n-terminal circuit disjunctive, and thus in avoiding sneak paths.