
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The basic laser equations
المؤلف:
H. HAKEN
المصدر:
LASER LIGHT DYNAMICS
الجزء والصفحة:
vol 2 ، p119
22-12-2016
2093
The basic laser equations
In this section we summarize the basic equations which we have derived in the preceding sections. In this way a reader not interested in their detailed derivation is enabled to start with these equations right from here. We first explain the quantities occurring in the laser equations. Such a quantity is the electric field strength of the light field in the laser. This function which depends on space and time is expanded into a superposition of resonator modes uλ(x). The index λ distinguishes the different modes. We assume that the cavity modes are normalized within the volume of the cavity and that they are orthogonal with respect to each other. We allow for an open cavity so that a cavity may consist of two mirrors mounted at the opposite ends of a laser rod. A one-dimensional example for such a mode is provided by a standing wave
 (1.1)
(1.1)
where eλ is a unit vector in the direction of the polarization of the electric field. kλ is the wave number and ⍵λ is the corresponding light frequency in the cavity without laser material. Finally we assume that the light field connected with the mode λ can stay only a finite time in the resonator. More precisely speaking we assume that the light field amplitude decays in the course of time by means of the damping constant kλ. Thus the electric field strength is represented in the form
 (1.2)
(1.2)
where bλ(t) is the amplitude of the field mode A. This amplitude is made dimensionless by means of the factor Nλ,
 (1.3)
(1.3)
The specific choice of NA was made so that we can establish a direct connection with the quantum theory of the light field. The reader is advised to remember in the following that bλ(t) is connected with the electric field strength of the mode A except for a numerical factor. While the light field represents one subsystem of the laser, the other subsystem is provided by matter. We assume that the laser material is built up of individual atoms which we distinguish by the index μ. With each atom μ a dipole moment p, is connected which we represent in the form
 (1.4)
(1.4)
In it ϑ12 is the dipole matrix element which is in quantum theory a prescribed and time independent quantity. Its precise definition is given. αμ(t) are time dependent functions which determine the temporal behavior of the dipole moments p,. Because p, and a, differ only by the constant vector ϑ12 we shall consider in the following a, (t) as a dimensionless dipole moment and shall also call it that way. When we consider a system of two-level atoms, the only additional atomic variable still necessary is the inversion d,. It is defined as difference of the occupation numbers of the upper and the lower level of the atom μ;
 (1.5)
(1.5)
So far we have discussed the subsystems, namely the modes on the one hand and the quantities describing matter on the other hand (dipole moment and inversion). These two subsystems interact with each other by means of the electric interaction between the electrons of the atoms and the electric field. This interaction is described by a coupling constant g which depends on the indices μ and A ;
 (1.6)
(1.6)
Evidently this coupling constant contains the dipole matrix element ϑ21 as well as the spatial field amplitude uλ taken at the atomic position xμ. This assumption implies the dipole approximation. As we have shown in the preceding sections, the following equations have been obtained for the fundamental equations by means of two approximations: namely the rotating wave approximation and the slowly varying amplitude approximation. The corresponding equations read:
(1) Field equations
 (1.7)
(1.7)
The physical content of these equations can be explained as follows. The 1.h.s. describes the temporal change of the field amplitude. The r.h.s. describes the causes of this change. The first two terms on the r.h.s. describe the oscillation and damping of the field amplitude in the resonator if there is no interaction between the field amplitude and the laser atoms present. The last term describes how the dipole moments act as a driving force on the oscillations of the field. The second group of equations refers to the atoms.
(2) Matter equations
 (1.8)
(1.8)
 (1.9)
(1.9)
In analogy to (1.7) the left-hand sides describe the temporal change of the dipole moments and the atomic inversion, respectively. We now discuss the right-hand sides which present the causes of the temporal changes of a, and d,. We discuss the first term in (1.8). This contains the transition frequency of the atom μ, i.e. 6,. Because in solids, atoms may occupy sites which are more or less different, the transition frequencies of the individual atoms may differ from each other. We take this fact into account by using the index μ. By the interaction of the atom with its surrounding the free oscillation of its dipole moment will be damped. The corresponding damping constant is denoted by y. The first term on the r.h.s. of (1.8) thus describes the oscillation and damping of the atomic dipole moment if no interaction with the light field takes place. The sum over A which occurs in (1.8) describes the interaction of all modes A with the atom under consideration. The factor dμ is of special importance. On account of it the laser equations become nonlinear because here the product between the two quantities bλ and dμ occurs. This term describes how the electric field represented by its mode amplitudes bλ drives the dipole moment. But because we are dealing here with a two-level atom, the energy flux between the atom and the field depends on the internal state of the atom. If its electron is in its upper state, energy will be transferred from the atom to the dipole moment. On the other hand if the atom is in its lower state, energy will be transferred from the field into the atom by absorption. This change of direction is taken care of by the factor dμ whose size depends on the actual occupancy of the two atomic levels. Let us now turn to a discussion of the r.h.s. of eq. (1.9). The first term describes the relaxation of the inversion caused by the pumping and incoherent relaxation processes. d0 represents the resulting equilibrium inversion and T is the corresponding relaxation time. The sum over A is brought about by the interaction between the field modes A and the atom μ. As may be shown this term is proportional to the energy per second put into the atom or drawn out of it because of the coherent interaction between the atom and the field. As we shall see in the next chapters, a wealth of phenomena is described by the equations (1.7) till (1.9). For sake of completeness we now quote a formulation, which is equivalent to eqs. (1.7)-(1.9), but which stresses the continuous distribution of atomic frequencies,  μ, in an inhomogeneously broadened atomic line. In such a description the frequency
μ, in an inhomogeneously broadened atomic line. In such a description the frequency  μ is replaced by the continuous (frequency) variable
μ is replaced by the continuous (frequency) variable  , and correspondingly also the index μ. It is further assumed gμλ is space independent. Therefore the equations (1.8) and (1.9) read in this notation
, and correspondingly also the index μ. It is further assumed gμλ is space independent. Therefore the equations (1.8) and (1.9) read in this notation
 (1.10)
(1.10)
Most important, the sum Σμ in (1.7) is transformed into an integral over which contains the frequency distribution ρ( ), which may be a Gaussian or, in some model calculations, a Lorentzian. In this way, (1.7) is transformed into
), which may be a Gaussian or, in some model calculations, a Lorentzian. In this way, (1.7) is transformed into
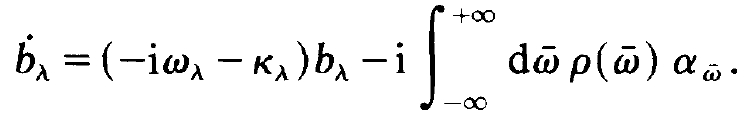 (1.11)
(1.11)
 الاكثر قراءة في مواضيع عامة في الليزر
الاكثر قراءة في مواضيع عامة في الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















