Derivation of the wave equation for the electric field strength

We start from the following Maxwell equations:

 (1.1)

 (1.2)

The first equation represents the induction law. It describes how vortices of the electric field strength E are caused by a temporal change of magnetic induction B. Eq. (1.2) describes how the current density j causes a vortex of the magnetic field H (Oersted's law). The vortex of the magnetic field can be caused by a temporal change of the dielectric displacement D, too. As usual we need the connections between D and E as well as between B and H. As is shown in electrodynamics, the dielectric displacement D depends on the electric field strength E via the polarization P of the medium in which the dielectric process takes place

    (1.3)

where ε₀ is the dielectric constant of the vacuum. We briefly remind the reader how to visualize the meaning of the polarization P. To this end we assume that the material is composed of individual atoms. When we apply an electric field, the electrons of the individual atoms will be displaced with respect to the atomic nuclei. Because the centers of the charges of the electrons and the nucleus do no more coincide, the applied electric field has induced a dipole at each individual atom. The polarization P is defined as the total dipole moment which stems from the individual atomic dipoles and is taken per unit volume. Later on it will be an important task of our theory to calculate the dipole moments of the individual atoms. Furthermore we wish to express the current density j by means of the electric field strength E. To this end we assume that the material or parts of it possess an electric conductivity σ and use Ohm's law. Therefore we may assume

    (1.4)

Finally we wish to confine our considerations to non-magnetic materials

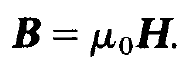   (1.5)

Furthermore we wish to treat wave phenomena and therefore we shall assume that the electric field is transversal which is equivalent to the assumption

 (1.6)

It will be our goal to derive a simple equation from the equations mentioned above, namely an equation for the electric field strength. If we know this quantity we may calculate, e.g. the magnetic induction by means of eq. (1.1). In our subsequent treatment we shall deal only with the electric field strength E because it contains all the information which we need to develop laser theory. In a first step we differentiate (1.2) with respect to time and obtain

 (1.7)

In (1.1) we replace the magnetic induction B by μ₀H Then we express H in (1.7) by curl E according to (1.1) and thus obtain for the 1.h.s. of (1.7)

 (1.8)

In deriving (1.8) we have used the following equation, well known from the vector calculus:

curl curl E = grad div E - AE,

where the relation (1.6) has been taken into account. In it A is as usual the Laplace operator, A = ∂²/∂x² + ∂²/∂y² + ∂²/∂z². Finally we replace the quantities j and D on the r.h.s. of (1.7) by means of the relations (1.4) and (1.3), respectively, and bring all expressions containing E to the 1.h.s. of (1.7). We thus obtain the fundamental wave equation

   (1.9)

where we have put ε₀ μ₀ = l/c², with c the light velocity in vacuum. When we put P = 0, (1.9) reduces to the telegraph equation which was derived in the last century. In the exercises we shall discuss some solutions of the telegraph equation. In eq. (1.9) the polarization P may be considered as a source term which produces the electric field. On the other hand an electric field in a medium can generate a polarization. Therefore we have to deal with the question how to calculate the polarization P.