Elementary Theory of integration -The Darboux Integral for Functions on R^N

The reader is undoubtedly familiar with the idea of the integral and with methods of performing integrations. In this section we define the integral precisely and prove the basic theorems for the processes of integration.

Let f be a bounded function whose domain is a closed interval I ={x : a ≤ x ≤ b}. We subdivide I by introducing points t₁,t₂,...,t_n−1 that are interior to I. Setting a = t₀ and b =t_n and ordering the points so that t₀ < t₁ <t₂ <...<t_n, we denote by I₁,I₂,...,I_n the intervals       I_i ={x : t_i−1 ≤ x ≤ t_i}. Two successive intervals have exactly one point in common. (See Figure 1.1.) We call such a decomposition of I into subintervals a subdivision of I, and we use the symbol Δ to indicate such a subdivision. Since f is bounded on I, it has a least upper bound (l.u.b.), denoted by M. The greatest lower bound (g.l.b.) of f on I is denoted by m. Similarly, M_i and mi denote the l.u.b. and g.l.b., respectively, of f on Ii . The length of the interval Ii is t_i − t_i−1; it is denoted by l(I_i).

Definitions

The upper Darboux sum of f with respect to the subdivision Δ , denoted S⁺(f,Δ), is defined by(1.1)

Similarly , the lower Darboux sum, denoted S−(f,Δ), is defined by(1.2)

                                                     Figure 1.1 A subdivision of I.

Suppose Δ is a subdivision a =t₀ <t₁ < ... < t _n−1 <t_n = b, with the corresponding intervals denoted by I₁,I₂,...,In. We obtain a new subdivision by introducing additional subdivision points between the various {ti}. This new subdivision will have subintervals I^/₁,I^/₂,...,I^/_m each of which is a part (or all) of one of the sub intervals of Δ. We denote this new subdivision by Δ^/and call it a refinement of .

Suppose that Δ₁ with subintervals I₁,I₂,...,In and that Δ₂ with subintervals J₁,J₂,...,J_m are two subdivisions of an interval I. Wegetanew subdivision of I by taking all then dpoints of the subintervals of bothΔ₁ and Δ₂, arranging them in order of increasing size, and then labeling each subinterval having as its endpoints two successive subdivision points. Such a subdivision is called the common refinement ofΔ₁ and Δ₂, and each subinterval of this new subdivision is of the form I_i ∩ J_k, i = 1, 2,...,n,    k = 1, 2,...,m. Each I_i ∩ J_k is either empty or entirely contained in a unique subinterval (Ii) of Δi and a unique subinterval (J_k) of Δ₂. An illustration of such a common refinement is exhibited in Figure

1.2.

Theorem 1.1

Suppose that f is a bounded function with domain I ={x:a ≤ x ≤ b}. Let Δ be a subdivision of I and suppose that M and m are the least upper bound and greatest lower bound of f on I, respectively. Then

(a)m(b − a) ≤ S−(f,Δ) ≤ S+(f,Δ) ≤ M(b − a).

(b) If Δ^/is a refinement of Δ, then S−(f,Δ) ≤ S−(f,Δ^/) ≤ S+(f,Δ^/) ≤ S+(f, Δ).

(c) If Δ₁ and Δ₂ are any two subdivisions of I, thenS−(f,Δ₁) ≤ S⁺(f,Δ₂).

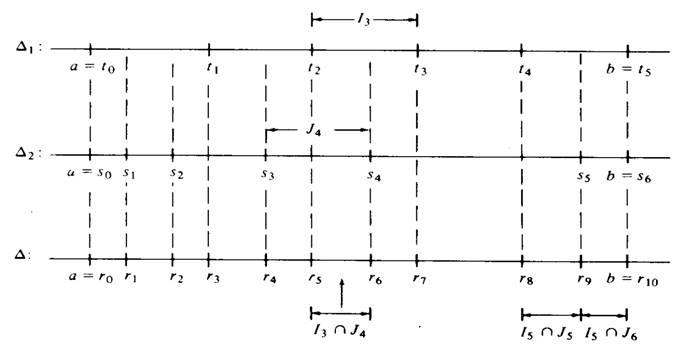
Figure 1.2 A common refinement.

Proof

(a) From the definition of least upper bound and greatest lower bound, we have

Also

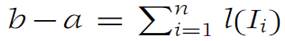
Thus the inequalities in part (a) are an immediate consequence of the definition of S⁺ and S− as given in equations (1.1) and(1.2):

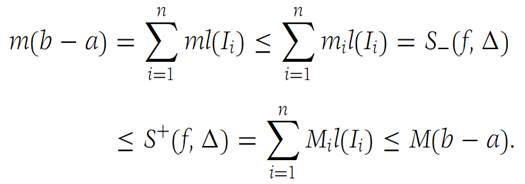
(b) To prove part (b), let Δi be the subdivision of Ii that consists of all those intervals of Δ^/ that lie in I_i . Since each interval of Δ^/ is in a unique Δ_i we have, applying part (a) to each Δi ,

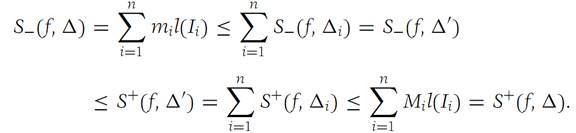
(c) To prove part (c), let Δ be the common refinement of Δ₁ and Δ₂. Then, using the result in part (b), we obtain

Definitions

If f is a function on R1 that is defined and bounded on I ={x : a ≤ x ≤ b}, we define its upper and lower Darboux integrals by

we say that f is Darboux integrable, or just integrable, on , and we designate the common value by

The following results are all direct consequences of the above definitions.

Theorem 1.2

If m  ≤ f(x) ≤ M for all x ∈ I ={x: a ≤ x ≤ b}, then

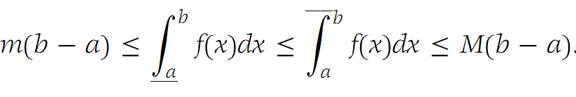
Proof

LetΔ₁ andΔ₂ be subdivisions of I. Then from parts (a) and (c) of Theorem 1.1, it follows that

We keep Δ₁ fixed and let Δ₂ vary over all possible subdivisions. Thus S⁺(f,Δ₂) is alwayslarger than or equal to S−(f,Δ₁), and so its greatest lower bound is alwayslarger than or equal to S−(f,Δ₁). We conclude that

Now letting Δ1 vary over all possible subdivisions, we see that the least upper bound of S−(f,Δ1) cannot exceed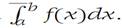The conclusion of the theorem follows.

The next theorem states simple facts about upper and lower Darboux integrals. The results all follow from the definitionsof inf, sup, and upper Darboux and lower Darboux integrals.

Theorem 1.3

Assuming that all functions below are bounded, we have the following formulas:(a) If g(x) = kf (x) for all x ∈ I ={x: a ≤ x ≤ b} and k is a positive number,

Then

Corollary

If the functions considered in Theorem 1.3 are Darboux  integrable, the following formulas hold:

1. If g(x)= kf (x) and k is any constant, then

1. If h(x) = f₁(x) + f₂(x), then

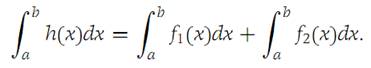
1. If f₁(x) ≤ f₂(x) for all x ∈ I, then

1. Suppose f is Darboux integrable on I₁ ={x: a ≤ x ≤ b} and on I₂ ={x: b ≤ x ≤ c}. Then it is Darboux integrable on I ={x: a ≤ x ≤ c}, and(1.3)

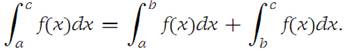
It is useful to define

Then formula (1.3) above is valid whether or not b is between a and c so long as all the integrals exist. It is important to be able to decide when a particular function is inte grable. The next theorem gives a necessary and sufficient condition for integrability.

Theorem 1.4

Suppose that f is bounded on an interval I ={x: a ≤ x ≤ b}. Then f is integrable ⇔ for every Ԑ> 0 there is a subdivision Δ of I such that

                           S+(f,Δ) −  S−(f,Δ) <Ԑ.

Suppose that condition (1.4) holds. Then from the definitions of upper and lower Darboux integrals, we have

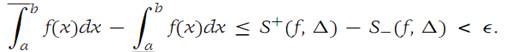
Since this inequality holds for every Ԑ> 0 and the left side of the inequality is independent of Ԑ, it follows that

Hence f is integrable.

Now assume that f is integrable; we wish to establish inequality (1.4).

For any Ԑ> 0 there are subdivisions Δ₁ and Δ2 such that(1.5)

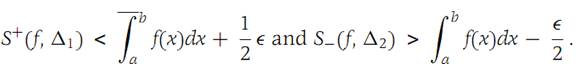
We choose Δ as the common refinement of Δ₁ and Δ₂. Then (from Theorem 1.1)

Substituting inequalities (1.5) into the above expression and using the fact that

As required.

If f is continuous on the closed interval I ={x: a ≤ x ≤ b}, then f is integrable.

The function f is uniformly continuous, and hence for any Ԑ> 0 there Is a δ such that

Choose a subdivision Δ of I such that no subinterval of Δ has length larger than δ. This allowsus to establish formula (1.4), and the result follows from Theorem 1.4.

Theorem 1.5(Mean-value theorem for integrals).

Suppose that f is continuous on I ={x: a ≤ x ≤ b}. Then there is a number ξ in I such that

According to Theorem 1.2, we have(1.6)

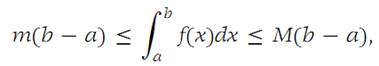
where m and M are the minimum and maximum of f on I, respectively. From the Extreme-value theorem there are numbers x₀ and x₁ ∈ I such that f(x₀)= m and f(x₁) =M. From inequalities (1.6) it follows that

where A is a number such that f(x₀) ≤ A ≤ f(x₁). Then the intermediate value theorem show that there is a number ξ ∈ I such that f(ξ)= A.

We now present two forms of the Fundamental theorem of calculus, a result that shows that differentiation and integration are inverse processes.

Theorem 1.6(Fundamental theorem of calculus—first form).

Suppose that f is continuous on I ={x:a ≤ x ≤ b}, and that F is defined by

Then F is continuous on I, and F^/(x) =f(x) for each x ∈ I₁ ={x: a<x<b}.

Since f is integrable on every subinterval of I, we have

We apply the Mean-value theorem for integrals(Theorem 1.5) to the last term on the right, getting

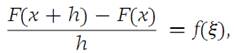
where ξ is some number between x and x + h. Now, let 8> 0 be given.

There is a δ> 0 such that |f(y) − f(x)| <Ԑ for all y on I1 (taking ξ y) with |y − x| <δ. Thus, if 0 < |h| <δ, we find that

Theorem 1.7(Fundamental theorem of calculus—second form).

Suppose that f and F are continuous on I ={x:a ≤ x ≤ b} and that F^/(x) = f(x) for each

x ∈ I₁ ={x:a<x<b}. Then(1.7)

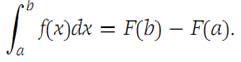
We consider a subdivision Δ of I. We write

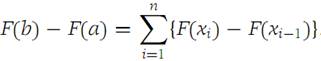
We apply the Mean-Value theorem to each term in the sum. Then as the

mesh size tends to zero we get (1.7).

1. Compute S⁺(f,Δ) and S−(f,Δ) for the function f : x → x2 defined on I ={x :0 ≤ x ≤ 1} where Δ is the subdivision of I into 5subintervals of equal size.

2. (a) Given the function f : x → x³ defined on I ={x :0 ≤ x ≤ 1},suppose Δ is a subdivision and Δ^/is a refinement of Δ that adds one more point. Show that S+(f,Δ^/)<S+(f,Δ) and S−(f,Δ^/)>S−(f, Δ).

(b) Give an example of a function f defined on I such that S+(f,Δ^/ ) = S+(f,Δ) and S−(f,Δ^/) =S−(f,Δ)

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(81-89)