
Basic Properties of Functions on R1 -Uniform Continuity
 المؤلف:
Murray H. Protter
المؤلف:
Murray H. Protter
 المصدر:
Basic Elements of Real Analysis
المصدر:
Basic Elements of Real Analysis
 الجزء والصفحة:
57-60
الجزء والصفحة:
57-60
 23-11-2016
23-11-2016
 1421
1421
In the definition of continuity of a function f at a point x0, it is necessary to obtain a number δ for each positive number ε prescribed in advance The number δ, which naturally depends on ε, also depends on the particular value x0. Under certain circumstances it may happen that the same value δ may be chosen for all points x in the domain. Then we say that f is uniformly continuous.
Definition
A function f with domain S is said to be uniformly continuous on S if for every ε> 0 there is a δ> 0 such that
|f(x1) − f(x2)| <ε whenever |x1 − x2| <δ
and x1,x2 are in S. The important condition of uniform continuity states that the same value of δ holds for all x1,x2 in S.
Among the properties of continuous functions used in proving the basic theorems of integral calculus, that of uniform continuity plays a central role. The principal result of this section (Theorem 1.1 below) shows that under rather simple hypotheses continuous functions are uniformly continuous.
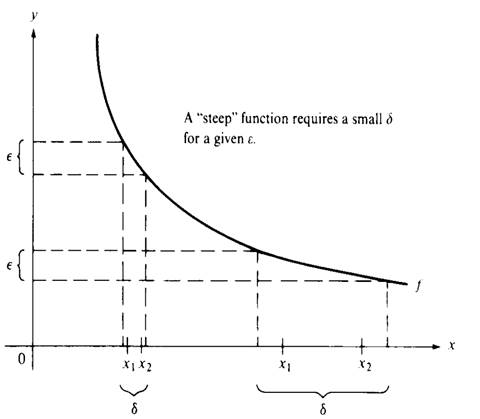
Figure 1.1
A function may be continuous on a set S without being uniformly continuous. As Figure 1.1 shows, once an ε is given, the value of δ required n the definition of ordinary continuity varies according to the location of x1 and x2; the “steeper” the function, the smaller the value of δ required. As an example of a continuous function that is not uniformly continuous, consider
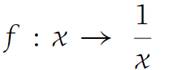
defined on the set S ={x :0 <x ≤ 1}. It is clear that f is continuous for each x in S. However, with ε any positive number, say 1, we shall show
there is no number δ such that
|f(x1) − f(x2)| < 1 whenever |x1 − x2| <δ
for all x1,x2 in S. To see this we choose x1 = 1/n and x2 = 1/(n + 1) for a positive integer n. Then |f(x1) − f(x2)|=|n − (n + 1)|= 1; also, we have |x1 − x2|= 1/(n(n + 1)).If n is very large, then x1 and x2 are close together. Therefore, if a δ is given, simply choose n so large that x1 and x2 are closer together than δ. The condition of uniform continuity is violated, since f(x1) and f(x2) may not be “close.”
An example of a uniformly continuous function on a set S is given by(1.6)

on the domain S ={x :0 ≤ x ≤ 1}. To see this, suppose ε> 0 is given.
We must find a δ> 0 such that
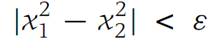
whenever |x1 − x2| <δ
for all x1,x2 in S. To accomplish this, choose δ = ε/2. Then, because 0 ≤ x1 ≤ 1 and 0 ≤ x2 ≤ 1, we have

This inequality holds for all x1,x2 on [0, 1] such that |x1 − x2| <δ.
The same function (1.6) above defined on the domain S1 ={x :0 ≤ x< ∞} is not uniformly continuous there. To see this, suppose ε> 0 Is given. Then for any δ> 0, choose x1,x2 such that x1 − x2 = δ/2 and x1 + x2 = 4ε/δ. Then we have

The condition of uniform continuity is violated for this x1,x2. An important criterion for determining when a function is uniformly continuous is established in the next result.
Theorem 1.1 (Uniform continuity Theorem)
If f is continuous on the closed interval I ={x:a ≤ x ≤ b}, then f is uniformly continuous on I.
Proof
We shall suppose that f is not uniformly continuous on I and reach a contradiction. If f is not uniformly continuous, there is an ε0 > 0for which there is no δ> 0 with the property that |f(x1) − f(x2)| <ε0 for all pairs x1,x2 ∈ I and such that |x1 − x2| <δ. Then for each positive integer n, there is a pair x/n,x//n on I such that(1.7)
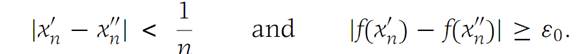
From the Bolzano–Weierstrass theorem, it follows that there is a subse-quence of {x/n}, which we denote {x/kn}, convergent to some number x0 in I. Then, since |x/kn− x//kn| < 1/n, we see that x//kn→ x0 as n →∞. Using the fact that f is continuous on I, we havef(x/kn) → f(x0), f(x//kn) → f(x0).
That is, there are positive integers N1 and N2 such that
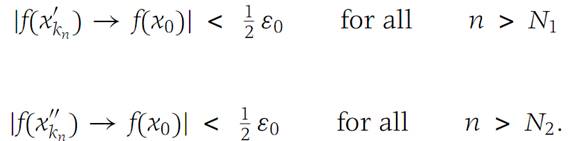
Hence for all n larger than both N1 and N2 we find
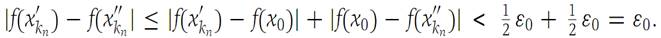
This last inequality contradicts (1.7), and the result is established. As the example of the function f : x → 1/x shows, the requirement that I be a closed interval is essential. Also, the illustration of the function f : x → x2 on the set S1 ={x :0 ≤ x< ∞} shows that Theorem1.11 does not apply if the interval is unbounded. It may happen that continuous functions are uniformly continuous on unbounded sets. But these must be decided on a case-by-case basis. See Problems 3 and 4 at the end of the section.
Problems
1. Suppose that f is a continuous, increasing function on a closed interval I ={x : a ≤ x ≤ b}. Show that the range of f is the interval [f(a), f(b)].
2. Suppose that f is uniformly continuous on the closed intervals I1
and I2. Show that f is uniformly continuous on S = I1 ∪ I2.
3. Show that the function f : x → 1/x is uniformly continuous on S ={x :1 ≤ x< ∞}.
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(57-60)
 الاكثر قراءة في التحليل الحقيقي
الاكثر قراءة في التحليل الحقيقي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


