EXAMPLE 1: ROCKET RAILROAD CAR. We recall this example, introduced in §1.2. We have

For

According to the Pontryagin Maximum Principle, there exists h≠0 such that

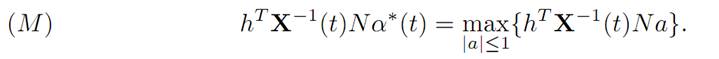
We will extract the interesting fact that an optimal control α^∗ switches at most one time.

We must compute e^tM. To do so, we observe

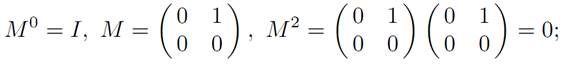
and therefore M^k = 0 for all k ≥ 2. Consequently,

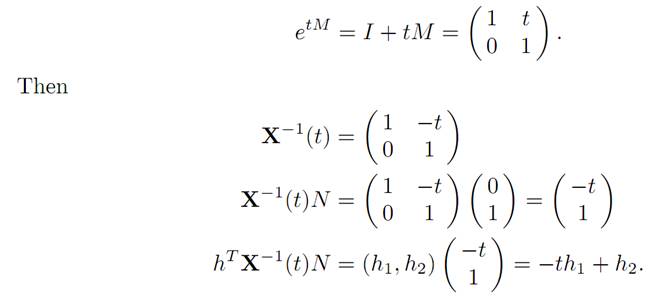
The Maximum Principle asserts

and this implies that

                 α^∗ (t) = sgn(−th₁ + h₂)

for the sign function

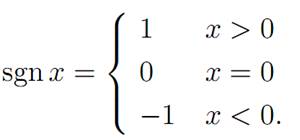
Therefore the optimal control α^∗ switches at most once; and if h₁ = 0, then α∗ is constant.

Since the optimal control switches at most once, then the control we constructed by a geometric method in §1.3 must have been optimal.

EXAMPLE 2: CONTROL OF A VIBRATING SPRING. Consider next the simple dynamics

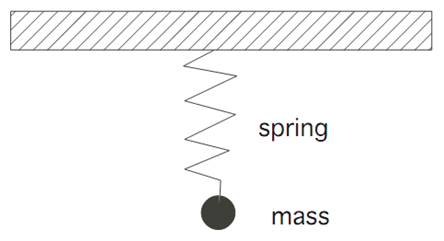
where we interpret the control as an exterior force acting on an oscillating weight  (of unit mass) hanging from a spring. Our goal is to design an optimal exterior forcing α^∗(.) that brings the motion to a stop in minimum time.

We have n = 2, m = 1. The individual dynamical equations read:

which in vector notation become

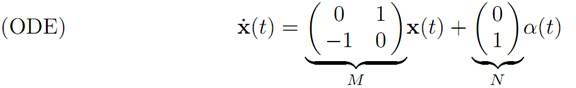
for |α(t)| ≤ 1. That is, A = [−1, 1].

Using the maximum principle. We employ the Pontryagin Maximum Principle, which asserts that there exists h ≠ 0 such that

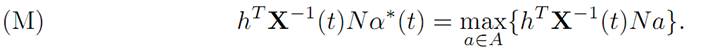
To extract useful information from (M) we must compute X(.). To do so, we observe that the matrix M is skew symmetric, and thus

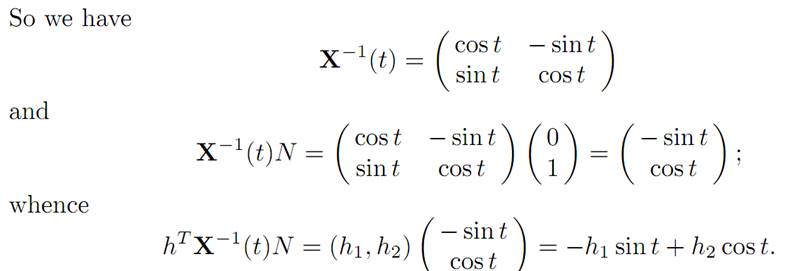
According to condition (M), for each time t we have

Therefore

α^∗(t) = sgn(−h₁ sin t + h₂ cos t).

Finding the optimal control. To simplify further, we may assume h²₁+h²₂ =1. Recall the trig identity sin(x + y) = sin x cos y + cos x sin y, and choose δ such that

−h₁ = cos δ, h₂ = sin δ. Then

α^∗ (t) = sgn(cos δ sin t + sin δ cos t) = sgn(sin(t + δ)).

We deduce therefore that α∗ switches from +1 to −1, and vice versa, every π units of time.

Geometric interpretation. Next, we figure out the geometric consequences.

When α ≡ 1, our (ODE) becomes

In this case, we can calculate that

Consequently, the motion satisfies (x¹(t) − 1)² + (x²)²(t) ≡ r²₁, for some radius r₁,  and therefore the trajectory lies on a circle with center (1, 0), as illustrated.

If α ≡ −1, then (ODE) instead becomes

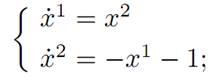
in which case

Thus (x¹(t)+1)² +(x²)²⁽t) = r²₂ for some radius r₂, and the motion lies on a circle with center (−1, 0).

In summary, to get to the origin we must switch our control α(.) back and forth between the values ±1, causing the trajectory to switch between lying on circles centered at (±1, 0). The switches occur each π units of time.

References

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.