
Space-Filling Geometry
 المؤلف:
Franklin Potter and Christopher Jargodzki
المؤلف:
Franklin Potter and Christopher Jargodzki
 المصدر:
Mad about Modern Physics
المصدر:
Mad about Modern Physics
 الجزء والصفحة:
p 22
الجزء والصفحة:
p 22
 7-10-2016
7-10-2016
 707
707
Space-Filling Geometry
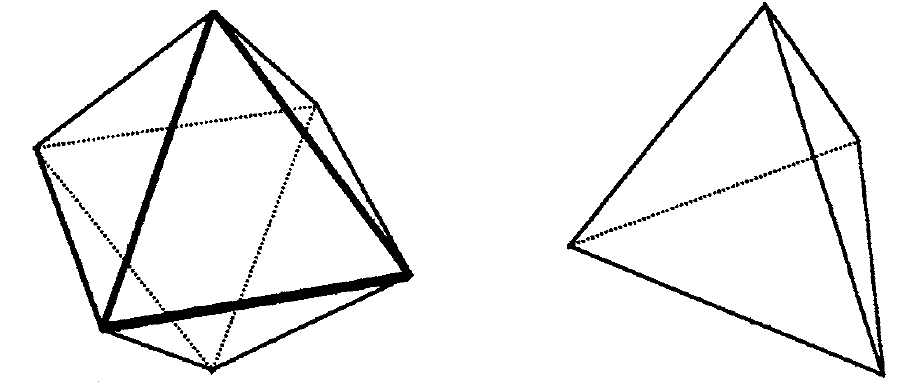
Cubes can be placed next to each other in three directions to fill all of 3D space. Regular octahedrons can fill 3D space also. Spheres of the same radius cannot. Can regular tetrahedrons fill all of D space and leave no gaps? Can regular dodecahedrons and regular icosahedrons?
Answer
First consider a two-dimensional flat space. A plane tesselation (or two dimensional honeycomb) is an infinite set of polygons fitting together to cover the whole plane once, with every side of each polygon belonging to just one other polygon. A regular tesselation has regular polygons. There are three regular tesselations of the plane: equilateral triangles, squares, and regular hexagons. There are additional plane tesselations with two or more convex polygon shapes. One also can cover the plane with Penrose tiles, polygon pairs with at least one polygon not being convex.
Now consider an additional spatial dimension. A three-dimensional honeycomb (or solid tesselation) is an infinite set of polyhedrons fitting together to fill all space once, so that every face of each polyhedron belongs to one other polyhedron. If we require all the polyhedrons to be identical, then the only regular honeycomb is the one filled with cubes, eight at each vertex. If we allow two different regular polyhedrons, one can fill the space with eight regular tetrahedrons and six regular octahedrons surrounding each vertex. These space fillings and others determine many of the natural crystal structures.
From the apparent simplicity of a 3D space filled with cubes, one may think that this solid tesselation would be the most likely mathematically if real space is discrete instead of continuous. However, mathematicians can show that the most likely and interesting 3D discrete space is the non-Euclidean tessellation by dodecahedrons, of which there are two kinds, depending on the angle of twist in relating one dodecahedron to the adjacent one. For further information see the Thurston and Weeks reference below.
 الاكثر قراءة في طرائف الفيزياء
الاكثر قراءة في طرائف الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


