Joule Cycle

Find the efficiency of the Joule cycle, consisting of two adiabats and two isobars (see Figure 1.1). Assume that the heat capacities of the gas C_P and C_V are constant.

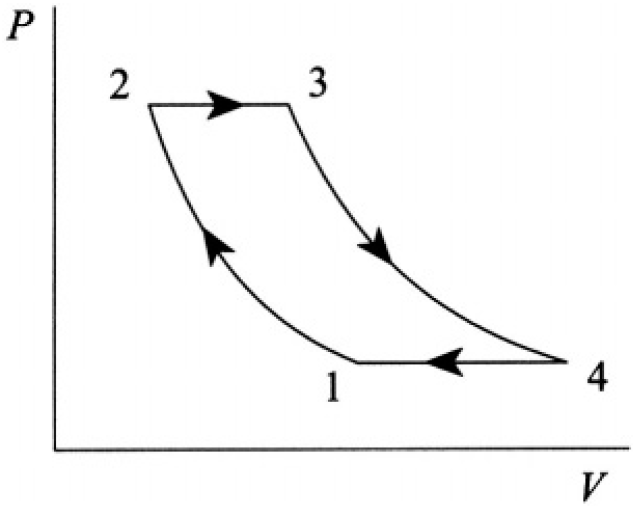
Figure 1.1

SOLUTION

The efficiency η of the cycle is given by the work W during the cycle divided by the heat Q absorbed in path 2 → 3 (see Figure 1.2). W is defined by the area enclosed by the four paths of the P–V plot. The integral ∫P dV along the paths of constant pressure 2 → 3 and 4→1 is simply the difference in volume of the ends times the pressure, and the work along the adiabats, where there is no heat transfer δQ = 0, is given by the change in internal energy C_VδT:

(1)

Figure 1.2

Substituting the ideal gas law PV = nRT into (1) and rearranging, we find

(2)

where we used C_P = C_V + nR. In the process 2 → 3, the gas absorbs the heat Q:

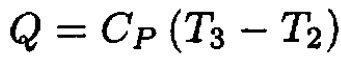(3)

What remains is to write W and Q in terms of P and form the quotient. Using the equation for an adiabatic process in an alternative form,

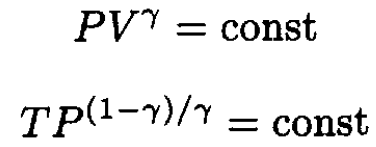
we have

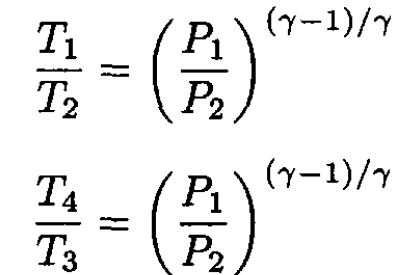(4)

Substituting for T₁ and T₄ by putting (4) into (1) yields

(5)

The efficiency η is then