


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 23-8-2016
Date: 19-8-2016
Date: 29-8-2016
|
Adiabatic Demagnetization
A paramagnetic sample is subjected to magnetic cooling.
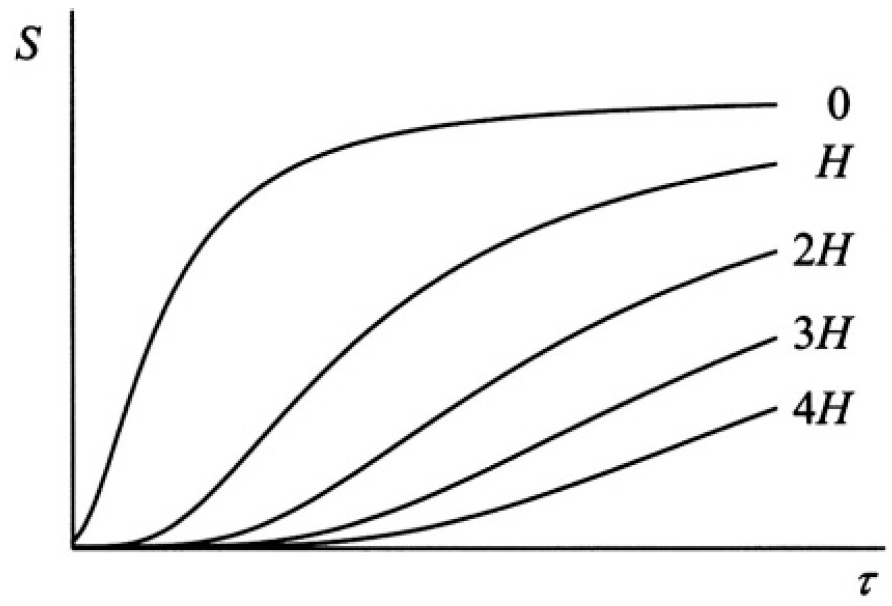
Figure 1.1
a) Show that
 (1)
(1)
Assume χ is independent of H. Show that
 (2)
(2)
where M = V χ H is the magnetization, χ is the isothermal magnetic susceptibility per unit volume, H is the magnetic field, and CH is the heat capacity at constant H.
b) For an adiabatic process, show that
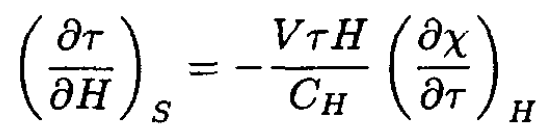 (3)
(3)
c) Assume that χ can be approximated by Curie’s law χ = a/τ and that the heat capacity at zero magnetic field is given by
 (4)
(4)
where a and b are constants. Show that
 (5)
(5)
For an adiabatic process, show that the ratio of final and initial temperatures is given by
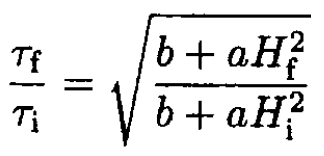 (6)
(6)
d) Explain and indicate in the S-τ diagram given in Figure 1.1 a possible route for the adiabatic demagnetization cooling process to approach zero temperature.
SOLUTION
a) We start with the usual relation dE = τ dS – P dV, and substitute M dH for P dV, since the work done in this problem is magnetic rather than mechanical. So
 (1)
(1)

Figure 1.2
We now want to produce a Maxwell relation whose independent variables are T and H. Write an equation for the free energy F:
 (2)
(2)
We then obtain, from (2),
 (3)
(3)
The cross derivatives of (3) are equal so
 (4)
(4)
The heat capacity at constant magnetic field is given by
 (5)
(5)
from which we obtain
 (6)
(6)
By again exchanging the order of differentiation in (6) and using the result found in (4), we have
 (7)
(7)
Replacing M by VχH in (7) yields the desired
 (8)
(8)
b) For an adiabatic process, the entropy S is constant. Writing S = S(τ, H), we compose the differential
 (9)
(9)
and by (4) and (5),
 (10)
(10)
c) The heat capacity CH(τ, H) may be written as the integral
 (11)
(11)
Substituting χ = a/τ into (8), we have
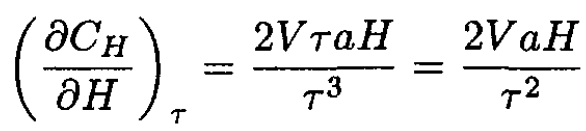 (12)
(12)
Using the heat capacity at zero magnetic field, CH(τ, 0) = V/τ2, and (12) in (11), we obtain
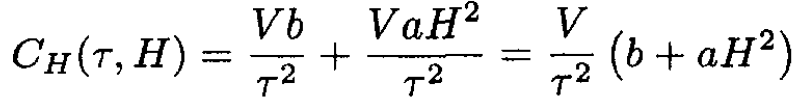 (13)
(13)
The temperature τ may be written τ = τ(S, H), so for our adiabatic process
 (14)
(14)
The integrand in (14) is found by substituting χ = a/τ into (10):
 (15)
(15)
So, for a process at constant entropy, we may write
 (16)
(16)
Rearranging and integrating give
 (17)
(17)
and
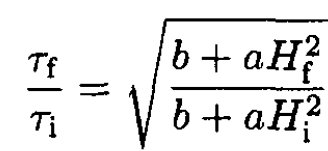 (18)
(18)
d) A possible route to zero temperature is illustrated in Figure 1.2. During leg 1 the paramagnetic sample is kept in contact with a reservoir at a low temperature, and the magnetic field is raised from 0 to H1. The contact with the reservoir is then removed, and the field is reduced to zero along leg 2. The sample is thereby cooled.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|