
Electronic spectra of octahedral and tetrahedral complexes
 المؤلف:
CATHERINE E. HOUSECROFT AND ALAN G. SHARPE
المؤلف:
CATHERINE E. HOUSECROFT AND ALAN G. SHARPE
 المصدر:
INORGANIC CHEMISTRY
المصدر:
INORGANIC CHEMISTRY
 الجزء والصفحة:
2th ed p 574
الجزء والصفحة:
2th ed p 574
 23-8-2016
23-8-2016
 2085
2085
Electronic spectra of octahedral and tetrahedral complexes
Electronic spectroscopy is a complicated topic and we shall restrict our discussion to high-spin complexes. The spectrum of [Ti)H2O(6]3+ (Figure1.1) exhibits one broad band; close inspection shows the presence of a shoulder indicating that the absorption is actually two closely spaced bands arising from a Jahn–Teller effect in the excited state.
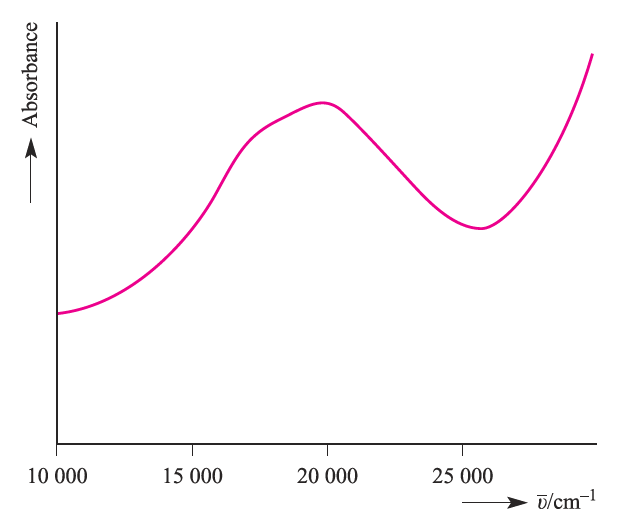
Fig. 1.1 The electronic spectrum of [Ti(H2O)6�]+3 in aqueous solution.
The term symbol for the ground state of Ti3+ (d1, one electron for which ml = 2, L = 2, S = 1/2 ) is 2D. In an octahedral field, this is split into 2T2g and 2Eg terms separated by energy Δoct, the magnitude of which increases with increasing field strength (Figure 1.2).

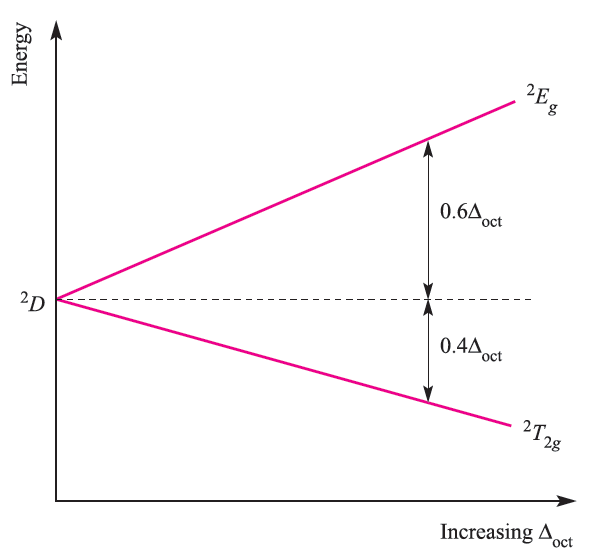
Fig. 1.2 Energy level diagram for a d1 ion in an octahedral field.
The electronic spectrum of Ti3+ arises from a transition from the T2g to Eg term; the energy of the transition depends on the field strength of the ligands in the octahedral Ti(III) complex. For the d9 configuration (e.g. Cu2+) in an octahedral field (actually, a rare occurrence because of Jahn–Teller effects which lower the symmetry), the ground state of the free ion (2D) is again split into 2T2g and 2Eg terms, but, in contrast to the d1 ion (Figure 20.16), the 2Eg term is lower than the 2T2g term. The d9 and d1 configurations are related by a positive hole concept: d9 is derived from a d10 configuration by replacing one electron by a positive hole; thus, whereas the d1 configuration contains one electron, d9 contains one ‘hole’ (see Box 20.6). For a d9 ion in an octahedral field, the splitting diagram is an inversion of that for the octahedral d1 ion. This relationship is shown in Figure 20.17 (an Orgel diagram) where the right-hand side describes the octahedral d1 case and the left-hand side, the octahedral d9 ion. Just as there is a relationship between the d1 and d9 configurations, there is a similar relationship between the d4 and d6 configurations. Further, we can relate the four configurations in an octahedral field as follows. In the weak-field limit, a d5 ion is high-spin and spherically symmetric, and in this latter regard, d0, d5 and d10 configurations are analogous. Addition of one electron to the high-spin d5 ion to give a d6 configuration mimics going from a d0 to d1 configuration; likewise, going from d5 to d4 by adding a positive hole mimics going from d10 to d9. The result is that the Orgel diagrams for octahedral d1 and d6 ions are the same, as are the diagrams for octahedral d4 and d9 (Figure 1.3).

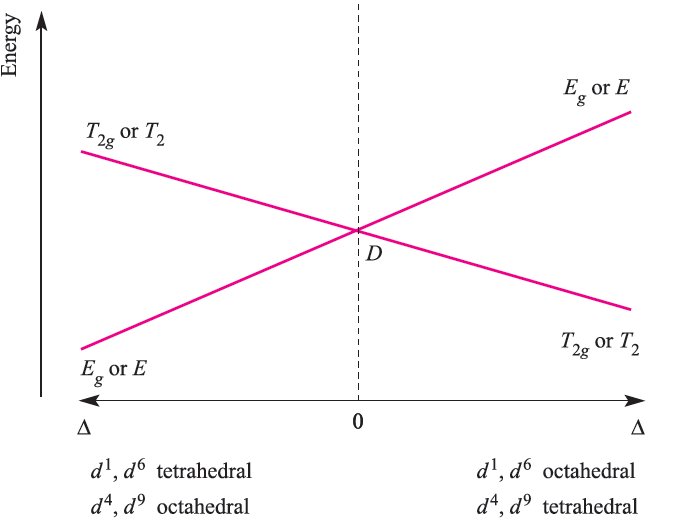
Fig. 1.3 Orgel diagram for d1, d4 (high-spin), d6 (highspin) and d9 ions in octahedral (for which T2g and Eg labels are relevant) and tetrahedral (E and T2 labels) fields. In contrast to Figure 1.2, multiplicities are not stated because they depend on the dn configuration.
Figure 1.3 also shows that the diagram for a d1 or d9 ion is inverted by going from an octahedral to tetrahedral field. Because the Orgel diagram uses a single representation for octahedral and tetrahedral fields, it is not possible to indicate that Δtet = 4/9Δoct. Tetrahedral d4 and d6 ions can also be represented on the same Orgel diagram.
Finally, Figure 20.17 shows that for each of the octahedral and tetrahedral d1, d4, d6 and d9 ions, only one electronic transition (see Box 20.3) from a ground to excited state is possible:
- for octahedral d1 and d6, the transition is Eg←T2g
- for octahedral d4 and d9, the transition is T2g←Eg
- for tetrahedral d1 and d6, the transition is T2←E
- for tetrahedral d4 and d9, the transition is E←T2
Each transition is spin-allowed (no change in total spin, S) and the electronic spectrum of each ion exhibits one absorption. For sake of completeness, the notation for the transitions given above should include spin multiplicities, 2S + 1, e.g. for octahedral d1, the notation is 2Eg←2T2g, and for high-spin, octahedral d4, 5T2g←5Eg. In an analogous manner to grouping d1, d4, d6 and d9 ions, we can consider together d 2, d3, d7 and d8 ions in octahedral and tetrahedral fields. Two terms arise for the d2 ion: 3F (ground state) and 3P (excited state); deriving terms from a table of microstates is dealt with in the next subsection. In an octahedral field, the 3P term does not split, and is labelled 3T1g. The 3F term splits into 3T1g, 3T2g and 3A2g terms. The 3T1g(F) term corresponds to a t2g 2eg0 arrangement and is triply degenerate because there are three ways of placing two electrons (with parallel spins) in any two of the dxy, dyz and dxz orbitals. The 3A2g term corresponds to t2g0 eg2 arrangement (singly degenerate).
The 3T2g and 3T1g)P( terms equate with a t2g1 eg1 configuration; the lower energy 3T2g term arises from placing two electrons in orbitals lying in mutually perpendicular planes, e.g. (dxy)1(dz2)1, while the higher energy 3T1g(P) term arises from placing two electrons in orbitals lying in the same plane e.g. (dxy)1(dx2-y2)1. The energies of the 3T1g(F), 3T2g, 3A2g and 3T1g(P( terms are shown on the right-hand side of Figure 20.18; note the effect of increasing field strength. Starting from this diagram and using the same arguments as for the d1, d4, d6 and d9 ions, we can derive the complete Orgel diagram shown in Figure 1.4. At increased field strengths, the lines describing the T1g(F) and T1g(P (terms (or T1, depending on whether we are dealing with octahedral or tetrahedral cases) curve away from one another; there is interaction between terms of the same symmetry and they are not allowed to cross (the non-crossing rule). From Figure 20.18, we can see why three absorptions are observed in the electronic spectra of d2, d3, d7 and d8 octahedral and tetrahedral complexes; the transitions are from the ground to excited states, and are all spin-allowed. Transitions are possible from one excited state to another, but their probability is so low that they can be ignored. Figure 20.19 illustrates spectra for octahedral nickel(II) (d8) complexes.
For the high-spin d5 configuration, all transitions are spinforbidden and ‘d–d’ transitions that are observed are between the 6S ground state and quartet states (three unpaired electrons).

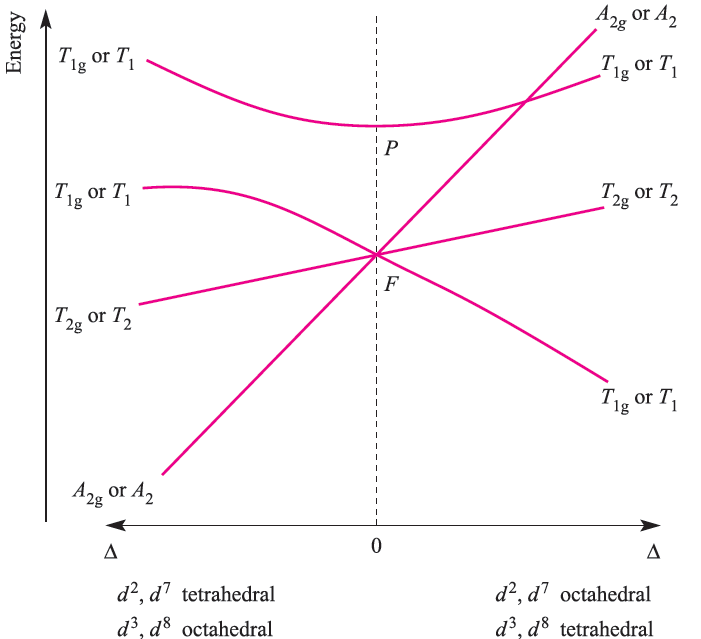
Fig. 1.4 Orgel diagram for d2, d3, d7 and d8 ions (highspin) in octahedral (for which T1g, T2g and A2g labels arerelevant) and tetrahedral (T1, T2 and A2 labels) fields. Multiplicities are not stated because they depend on the d n configuration, e.g. for the octahedral d2 ion, 3T1g, 3T2g and 3A2g labels are appropriate.
Associated absorptions are extremely weak. For a proper interpretation of electronic spectral features, interelectronic interaction must be taken into account and parameters additional to Δoct are needed to quantify the description of the spectrum. There are Racah parameters which we shall meet again when we describe Tanabe–Sugano diagrams. The evaluation of Δoct from electronic spectra is, therefore, more difficult for d2 (and related dn) than for d1 (and d6 etc.) ions and some uncertainty is often associated with reported values.
Worked example Electronic spectra
The electronic spectrum of an aqueous solution of [Ni(en)3]2+ exhibits broad absorptions with λmax ≈ 325, 550 and 900 nm.
(a) Suggest assignments for the electronic transitions. (b)Which bands are in the visible region?
(a) [Ni(en)3]2+ is a Ni(II), d8 complex. From the Orgel
diagram in Figure 20.18 the three transitions can be assigned; lowest wavelength corresponds to highest energy transition:

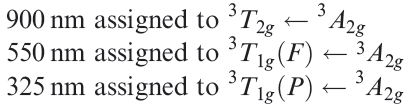
(b) Visible region spans ≈ 400–750 nm, so only the 550nm absorption falls in this range.

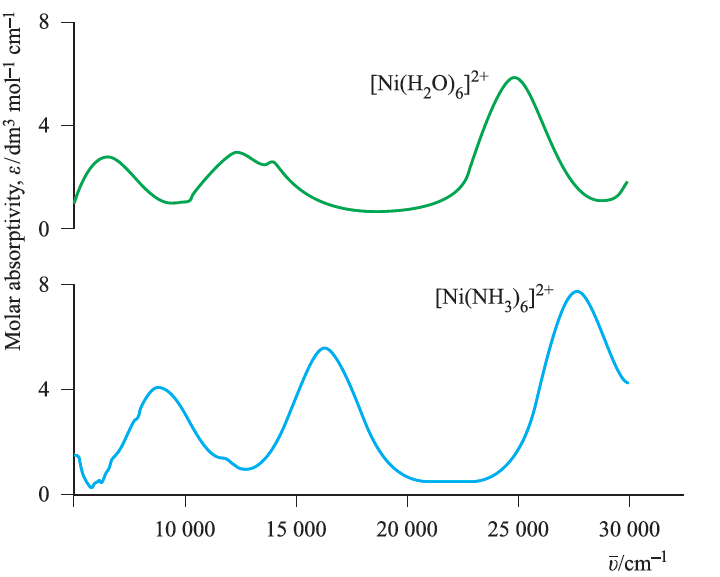
Fig. 1.5 Electronic spectra of [Ni(H2O)6]2+ (0.101 mol dm -3) and [Ni(NH3)6]2+ (0.315 mol dm -3 in aqueous NH3 solution) showing three absorption bands. Values of the molar absorptivity, ", are related to absorbance by the Beer–Lambert Law (equationbelow).
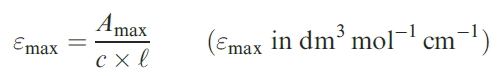
[This figure is based on data provided by Christian Reber; see: M. Triest, G. Bussie` re, H. Be´ lisle and C. Reber (2000) J. Chem. Ed., vol. 77, p. 670; http://jchemed.chem.wisc.edu/JCEWWW/ Articles/JCENi/JCENi.html]
 الاكثر قراءة في كيمياء العناصر الانتقالية ومركباتها المعقدة
الاكثر قراءة في كيمياء العناصر الانتقالية ومركباتها المعقدة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


