


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-8-2016
Date: 30-8-2016
Date: 9-8-2016
|
Spin–Orbit Interaction
Consider in three dimensions an electron in a harmonic oscillator potential which is perturbed by the spin–orbit interaction
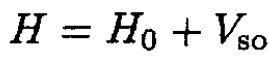 (i)
(i)
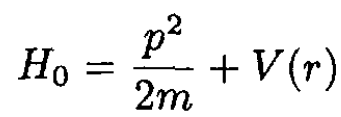 (ii)
(ii)
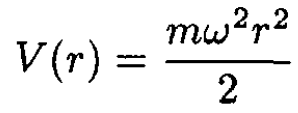 (iii)
(iii)
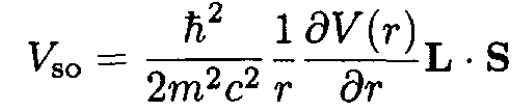 (iiii)
(iiii)
a) What are the eigenvalues of the ground state and the lowest excited states of the three-dimensional harmonic oscillator?
b) Use perturbation theory to estimate how these eigenvalues are altered by the spin–orbit interaction.
SOLUTION
a) In three dimensions the lowest eigenvalue of the harmonic oscillator is (3/2)hω, which can be viewed as hω/2 from each of the three dimensions. The ground state has s-wave symmetry. The lowest excited states have eigenvalue (5/2)hω. There are three of them. They have p-wave symmetry and are the states L = 1 and ML = (1,0, -1).
b) In the spin–orbit interaction we take the derivative ∂V/∂r and find
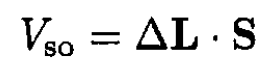 (1)
(1)
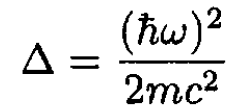 (2)
(2)
The matrix element ∆ is a constant, which simplifies the calculation. We evaluate the factor L . S by defining the total angular momentum J as
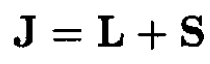 (3)
(3)
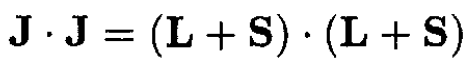 (4)
(4)
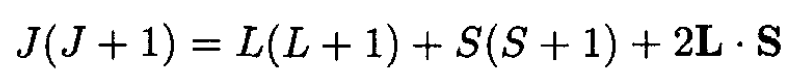 (5)
(5)
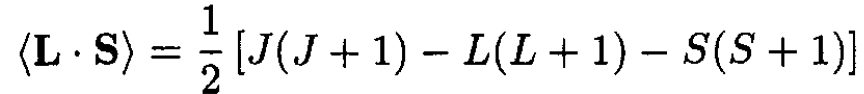 (6)
(6)
For the ground state of the harmonic oscillator, L = 0 and J = S = 1/2. The above expectation value of L . S is zero. The ground state is unaffected by the spin–orbit interaction, although it is affected by relativistic corrections as well as by other states.
The first excited states have L = 1, S = 1/2 so that J = 3/2, 1/2. For J = 3/2 we find that
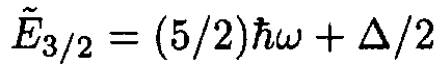 (7)
(7)
For J = 1/2 we find that
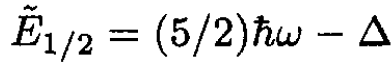 (8)
(8)



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|